
【題目】雙曲線![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,直線
,直線![]() 過
過![]() 且與雙曲線交于
且與雙曲線交于![]() 、
、![]() 兩點.
兩點.
(1)若![]() 的傾斜角為
的傾斜角為![]() ,
,![]() ,
,![]() 是等腰直角三角形,求雙曲線的標準方程;
是等腰直角三角形,求雙曲線的標準方程;
(2)![]() ,
,![]() ,若
,若![]() 的斜率存在,且
的斜率存在,且![]() ,求
,求![]() 的斜率;
的斜率;
(3)證明:點![]() 到已知雙曲線的兩條漸近線的距離的乘積為定值
到已知雙曲線的兩條漸近線的距離的乘積為定值![]() 是該點在已知雙曲線上的必要非充分條件.
是該點在已知雙曲線上的必要非充分條件.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)將![]() 代入雙曲線的方程,得出
代入雙曲線的方程,得出![]() ,由
,由![]() 是等腰直角三角形,可得出
是等腰直角三角形,可得出![]() ,再將
,再將![]() 代入可得出
代入可得出![]() 的值,由此可得出雙曲線的標準方程;
的值,由此可得出雙曲線的標準方程;
(2)先求出雙曲線的標準方程,并設直線![]() 的方程為
的方程為![]() ,將該直線的方程與雙曲線的方程聯立,列出韋達定理,并求出線段
,將該直線的方程與雙曲線的方程聯立,列出韋達定理,并求出線段![]() 的中點
的中點![]() 的坐標,由
的坐標,由![]() 得出
得出![]() ,轉化為
,轉化為![]() ,利用這兩條直線斜率之積為
,利用這兩條直線斜率之積為![]() ,求出實數
,求出實數![]() 的值,可得出直線
的值,可得出直線![]() 的斜率;
的斜率;
(3)設點![]() ,雙曲線的兩條漸近線方程為
,雙曲線的兩條漸近線方程為![]() ,利用點到直線的距離公式、雙曲線的方程以及必要不充分條件的定義,即可得證.
,利用點到直線的距離公式、雙曲線的方程以及必要不充分條件的定義,即可得證.
(1)直線![]() 的傾斜角為
的傾斜角為![]() ,
,![]() ,可得直線
,可得直線![]() ,代入雙曲線方程可得
,代入雙曲線方程可得![]() ,
,
![]() 是等腰直角三角形可得
是等腰直角三角形可得![]() ,即有
,即有![]() ,
,
解得![]() ,
,![]() ,則雙曲線的方程為
,則雙曲線的方程為![]() ;
;
(2)由![]() ,
,![]() ,可得
,可得![]() ,
,
直線![]() 的斜率存在,設為
的斜率存在,設為![]() ,設直線方程為
,設直線方程為![]() ,
,
![]() ,可得
,可得![]() ,
,
由![]() ,聯立雙曲線方程
,聯立雙曲線方程![]() ,
,
可得![]() ,
,
可得![]() ,線段
,線段![]() 的中點
的中點![]() 為
為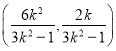 ,
,
由![]() ,可得
,可得![]() ,
,
解得![]() ,滿足
,滿足![]() ,故直線
,故直線![]() 的斜率為
的斜率為![]() ;
;
(3)證明:設![]() ,雙曲線的兩條漸近線為
,雙曲線的兩條漸近線為![]() ,
,
可得![]() 到漸近線的距離的乘積為
到漸近線的距離的乘積為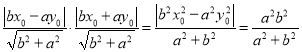 ,
,
即為![]() ,可得
,可得![]() ,
,
可得![]() 在雙曲線
在雙曲線![]() 或
或![]() 上,
上,
即有點![]() 到已知雙曲線的兩條漸近線的距離的乘積為定值
到已知雙曲線的兩條漸近線的距離的乘積為定值![]() 是該點在已知雙曲線上的必要非充分條件.
是該點在已知雙曲線上的必要非充分條件.


 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)如圖,在邊長為![]() 的菱形
的菱形![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 的中點,
的中點,![]() .沿
.沿![]() 將△
將△![]() 翻折到△
翻折到△![]() ,連接
,連接![]() ,得到如圖的五棱錐
,得到如圖的五棱錐![]() ,且
,且![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年某地初中畢業升學體育考試規定:考生必須參加長跑.擲實心球.1分鐘跳繩三項測試,三項測試各項20分,滿分60分.某學校在初三上學期開始時,為掌握全年級學生1分鐘跳繩情況,按照男女比例利用分層抽樣抽取了100名學生進行測試,其中女生54人,得到下面的頻率分布直方圖,計分規則如表1:
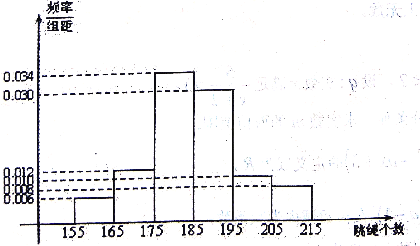

(1)規定:學生1分鐘跳繩得分20分為優秀,在抽取的100名學生中,男生跳繩個數大等于185個的有28人,根據已知條件完成表2,并根據這100名學生測試成績,能否有99%的把握認為學生1分鐘跳繩成績優秀與性別有關?
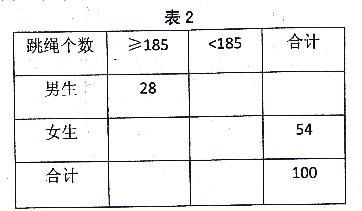
附:參考公式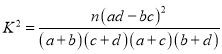
臨界值表:

(2)根據往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數都有明顯進步.假設今年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個,全年級恰有2000名學生,所有學生的跳繩個數X服從正態分布N(μ,σ2)(用樣本數據的平值和方差估計總體的期望和方差,各組數據用中點值代替)
①估計正式測試時,1分鐘跳182個以上的人數(結果四舍五入到整數);
②若在全年級所有學生中任意選取3人,正式測試時1分鐘跳195個以上的人數為ξ,求ξ占的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:
①函數![]() 的單調增區間是
的單調增區間是![]() ;
;
②若函數![]() 定義域為
定義域為![]() 且滿足
且滿足![]() ,則它的圖象關于
,則它的圖象關于![]() 軸對稱;
軸對稱;
③函數![]() 的值域為
的值域為![]() ;
;
④函數![]() 的圖象和直線
的圖象和直線![]() 的公共點個數是
的公共點個數是![]() ,則
,則![]() 的值可能是
的值可能是![]() ;
;
⑤若函數![]() 在
在![]() 上有零點,則實數
上有零點,則實數![]() 的取值范圍是
的取值范圍是![]() .
.
其中正確的序號是_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的參數方程是
的參數方程是 (m>0,t為參數),曲線
(m>0,t為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與曲線
,與曲線![]() 交于點
交于點![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正六棱錐![]() 的底面邊長為
的底面邊長為![]() ,高為
,高為![]() .現從該棱錐的
.現從該棱錐的![]() 個頂點中隨機選取
個頂點中隨機選取![]() 個點構成三角形,設隨機變量
個點構成三角形,設隨機變量![]() 表示所得三角形的面積.
表示所得三角形的面積.
(1)求概率![]() 的值;
的值;
(2)求![]() 的分布列,并求其數學期望
的分布列,并求其數學期望![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了了解學生對電子競技的興趣,從該校高二年級的學生中隨機抽取了![]() 人進行檢查,已知這
人進行檢查,已知這![]() 人中有
人中有![]() 名男生對電子競技有興趣,而對電子競技沒興趣的學生人數與電子競技競技有興趣的女生人數一樣多,且女生中有
名男生對電子競技有興趣,而對電子競技沒興趣的學生人數與電子競技競技有興趣的女生人數一樣多,且女生中有![]() 的人對電子競技有興趣.
的人對電子競技有興趣.
![]() 在被抽取的女生中與
在被抽取的女生中與![]() 名高二
名高二![]() 班的學生,其中有
班的學生,其中有![]() 名女生對電子產品競技有興趣,先從這
名女生對電子產品競技有興趣,先從這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人,求其中至少有
人,求其中至少有![]() 人對電子競技有興趣的概率;
人對電子競技有興趣的概率;
![]() 完成下面的
完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“電子競技的興趣與性別有關”.
的把握認為“電子競技的興趣與性別有關”.
有興趣 | 沒興趣 | 合計 | |
男生 | |||
女生 | |||
合計 |
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: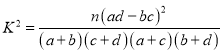
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一個特定時段內,以點E為中心的7海里以內海域被設為警戒水域.點E正北55海里處有一個雷達觀測站A.某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距![]() 海里的位置B,經過40分鐘又測得該船已行駛到點A北偏東
海里的位置B,經過40分鐘又測得該船已行駛到點A北偏東![]()
 且與點A相距
且與點A相距![]() 海里的位置C.
海里的位置C.
(1)求該船的行駛速度(單位:海里/時);
(2)若該船不改變航行方向繼續行駛判斷它是否會進入警戒水域,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com