【題目】已知
，
，且
對
恒成立，則
的最大值是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】分析：先求出函數的導數，再分別討論a=0，a＜0，a＞0的情況，從而得出ab的最大值．
詳解：令f（x）=ex-a（x-1）-b，則f′（x）=ex-a，
若a=0，則f（x）=ex-b≥-b≥0，得b≤0，此時ab=0；
若a＜0，則f′（x）＞0，函數單調增，x→-∞，此時f（x）→-∞，不可能恒有f（x）≥0．
若a＞0，由f′（x）=ex-a=0，得極小值點x=lna，
由f（lna）=a-alna+a-b≥0，得b≤a（2-lna），ab≤a2（2-lna）．令g（a）=a2（2-lna）．則g′（a）=2a（2-lna）-a=a（3-2lna）=0，得極大值點a=
．而g（）=
∴ab的最大值是故選C
名校練考卷期末沖刺卷系列答案科目：高中數學 來源： 題型：
【題目】已知點A(0，－2)，橢圓E： 
(a>b>0)的離心率為
，F是橢圓E的右焦點，直線AF的斜率為
，O為坐標原點.
(1)求E的方程；
(2)設過點A的動直線l與E相交于P，Q兩點.當△OPQ的面積最大時，求l的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若無窮數列
滿足：只要
，必有
，則稱
具有性質
.
（1）若
具有性質
，且
， 
，求
；
（2）若無窮數列
是等差數列，無窮數列
是公比為正數的等比數列， 
， 
， 
判斷
是否具有性質
，并說明理由；
（3）設
是無窮數列，已知
.求證：“對任意
都具有性質
”的充要條件為“
是常數列”.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】唐詩是中國文學的瑰寶.為了研究計算機上唐詩分類工作中檢索關鍵字的選取，某研究人員將唐詩分成7大類別，并從《全唐詩》48900多篇唐詩中隨機抽取了500篇，統計了每個類別及各類別包含“花”、“山”、“簾”字的篇數，得到下表：
愛情婚姻 | 詠史懷古 | 邊塞戰爭 | 山水田園 | 交游送別 | 羈旅思鄉 | 其他 | 總計 | |
篇數 | 100 | 64 | 55 | 99 | 91 | 73 | 18 | 500 |
含“山”字的篇數 | 51 | 48 | 21 | 69 | 48 | 30 | 4 | 271 |
含“簾”字的篇數 | 21 | 2 | 0 | 0 | 7 | 3 | 5 | 38 |
含“花”字的篇數 | 60 | 6 | 14 | 17 | 32 | 28 | 3 | 160 |
（1）根據上表判斷，若從《全唐詩》含“山”字的唐詩中隨機抽取一篇，則它屬于哪個類別的可能性最大，屬于哪個類別的可能性最小，并分別估計該唐詩屬于這兩個類別的概率；
（2）已知檢索關鍵字的選取規則為：
①若有超過95%的把握判斷“某字”與“某類別”有關系，則“某字”為“某類別”的關鍵字；
②若“某字”被選為“某類別”關鍵字，則由其對應列聯表得到的
的觀測值越大，排名就越靠前；
設“山”“簾”“花”和“愛情婚姻”對應的觀測值分別為
，
，
.已知
，
，請完成下面列聯表，并從上述三個字中選出“愛情婚姻”類別的關鍵字并排名.
屬于“愛情婚姻”類 | 不屬于“愛情婚姻”類 | 總計 | |
含“花”字的篇數 | |||
不含“花”的篇數 | |||
總計 |
附：
，其中
.
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“微信運動”是手機
推出的多款健康運動軟件中的一款，某學校140名老師均在微信好友群中參與了“微信運動”，對運動10000步或以上的老師授予“運動達人”稱號，低于10000步稱為“參與者”，為了解老師們運動情況，選取了老師們在4月28日的運動數據進行分析，統計結果如下：
運動達人 | 參與者 | 合計 | |
男教師 | 60 | 20 | 80 |
女教師 | 40 | 20 | 60 |
合計 | 100 | 40 | 140 |
（Ⅰ）根據上表說明，能否在犯錯誤概率不超過0.05的前提下認為獲得“運動達人”稱號與性別有關？
（Ⅱ）從具有“運動達人”稱號的教師中，采用按性別分層抽樣的方法選取10人參加全國第四屆“萬步有約”全國健走激勵大賽某賽區的活動，若從選取的10人中隨機抽取3人作為代表參加開幕式，設抽取的3人中女教師人數為
，寫出的分布列并求出數學期望
.
參考公式：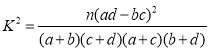
，其中
.
參考數據：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
上點
處的切線方程為
．
（Ⅰ）求拋物線的方程；
（Ⅱ）設
和
為拋物線上的兩個動點，其中
且
，線段
的垂直平分線
與
軸交于點
，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的一個頂點和兩個焦點構成的三角形的面積為4．
（1）求橢圓
的方程；
（2）已知直線
與橢圓交于
、
兩點，試問，是否存在
軸上的點
，使得對任意的
，
為定值，若存在，求出
點的坐標，若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某手機企業為確定下一年度投入某種產品的研發費用，統計了近
年投入的年研發費用
千萬元與年銷售量
千萬件的數據，得到散點圖1，對數據作出如下處理：令
，
，得到相關統計量的值如圖2：
（1）利用散點圖判斷
和
哪一個更適合作為年研發費用和年銷售量的回歸類型（不必說明理由），并根據數據，求出與的回歸方程；
（2）已知企業年利潤
千萬元與
的關系式為
（其中
為自然對數的底數），根據（1）的結果，要使得該企業下一年的年利潤最大，預計下一年應投入多少研發費用？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種設備隨著使用年限的增加，每年的維護費相應增加現對一批該設備進行調查，得到這批設備自購入使用之日起，前5年平均每臺設備每年的維護費用大致如下表：
年份 | 1 | 2 | 3 | 4 | 5 |
維護費 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
（1）在這5年中隨機抽取兩年，求平均每臺設備每年的維護費用至少有1年多于2萬元的概率；
（2）求
關于
的線性回歸方程．若該設備的價格是每臺16萬元，你認為應該使用滿五年換一次設備，還是應該使用滿八年換一次設備？請說明理由．
參考公式：用最小二乘法求線性回歸方程
的系數公式
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
