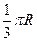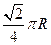如圖,在正三棱柱
ABC—
A1B1C1中,底面邊長為
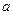
,
D為
BC中點,
M在
BB1上,且
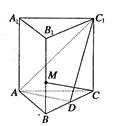
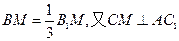
.
(1)求證:
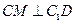
;
(2)求四面體
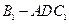
的體積.
(1)在正三棱柱ABC—A
1B
1C
1中,D為BC的中點,
則AD
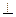
面BCC
1B
1,從而AD
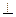
MC …………(2分)
又
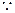
CM
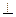
AC
1,則MC和平面ADC
1內兩相交直線AD,AC
1均垂直,
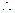
MC
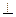
面ADC
1, …………(4分)
于是MC
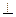
DC
1. …………(6分)
(2)在矩形BB
1C
1C中,由CM
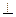
DC
1知
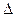
DCC
1~
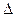
MBC,設BB
1=h,則BM=
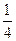
h.
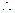
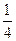
h:a=
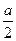
:h,求得h=
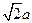
.從而所求AA
1=
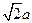
. …………(8分)
連結
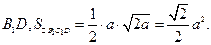
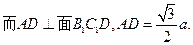
…………(10分)
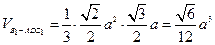
…………(12分)
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
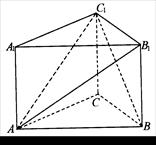
(本小題滿分12分)如圖,在直三棱柱ABC—A
1B
1C
1中,∠ACB=90°,AC=BC=CC
1=2.
(I)證明:AB
1⊥BC
1;
(II)求點B到平面AB
1C
1的距離;
(III)求二面角C
1—AB
1—A
1的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
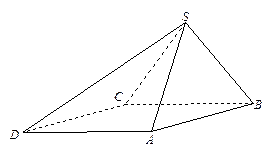
四棱錐
S—
ABCD中,底面
ABCD為平行四邊形,側面
SBC⊥底面
ABCD,已知
∠
ABC = 45°
AB=2,
BC=
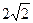
,
SA=
SB =
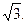
(Ⅰ)證明
SA⊥
BC;
(Ⅱ)求直線
SD與平面
SAB所成角的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分13分)
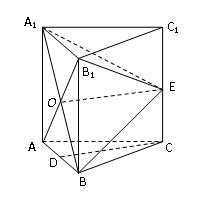
如圖,在三棱柱
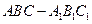
中,每個側面均為正方形,
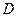
為底邊
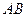
的中點,
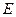
為側棱
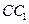
的中點,
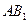
與
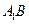
的交點為
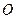
.
(Ⅰ)求證:
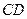
∥平面
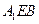
;
(Ⅱ)求證:
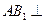
平面
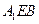
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
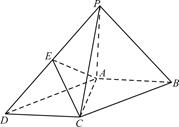
如圖,在底面為平行四邊形的四棱錐
P—
ABCD中,
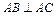
,
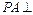
平面

,且
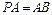
,點
E是
PD的中點.
(1)證明:
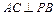
;
(2)證明:
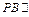
平面
AEC;
(3)求二面角
E—
AC—
B的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,是一個無蓋的正方體盒子展開后的平面圖,
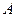
、
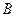
、
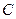
是展
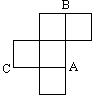
開圖上的三點, 則正方體盒子中
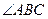
的值為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
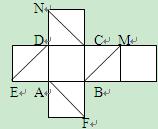
如圖是正方體的展開圖,在此正方體中:①BM//平面DEA;②CN//平面ABF;③平面BDM//平面AFN;④平面BDE//平面NCF。以上4個命題中,正確命題的序號是__________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在直三棱柱
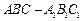
中,
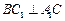
.有下列條件:
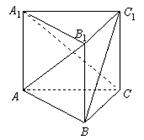
①
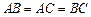
;②
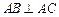
;③
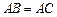
.其中能成為

的充要條件的是(填上該條件的序號)________。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在北緯45°的緯線圈上有

兩地,分別在東經(jīng)70°與東經(jīng)160°的經(jīng)線上,設地球半徑為
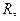
則

兩地的球面距離等于( )



查看答案和解析>>

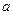 ,D為BC中點,M在BB1上,且
,D為BC中點,M在BB1上,且
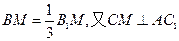 .
.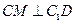 ;
;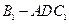 的體積.
的體積.
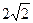 ,SA=SB =
,SA=SB =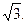

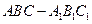 中,每個側面均為正方形,
中,每個側面均為正方形,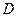 為底邊
為底邊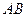 的中點,
的中點,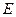 為側棱
為側棱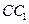 的中點,
的中點,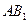 與
與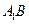 的交點為
的交點為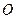 .
.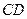 ∥平面
∥平面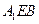 ;
; 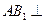 平面
平面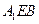 .
.

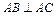 ,
,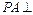 平面
平面 ,且
,且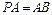 ,點E是PD的中點.
,點E是PD的中點.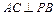 ;
;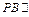 平面AEC;
平面AEC;
 兩地,分別在東經(jīng)70°與東經(jīng)160°的經(jīng)線上,設地球半徑為
兩地,分別在東經(jīng)70°與東經(jīng)160°的經(jīng)線上,設地球半徑為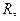 則
則 兩地的球面距離等于( )
兩地的球面距離等于( )