
【題目】已知由n(n∈N*)個正整數構成的集合A={a1,a2,…,an}(a1<a2<…<an,n≥3),記SA=a1+a2+…+an,對于任意不大于SA的正整數m,均存在集合A的一個子集,使得該子集的所有元素之和等于m.
(1)求a1,a2的值;
(2)求證:“a1,a2,…,an成等差數列”的充要條件是“![]() ”;
”;
(3)若SA=2020,求n的最小值,并指出n取最小值時an的最大值.
【答案】(1)a1=1,a2=2;(2)證明見解析;(3)n最小值為11,an的最大值1010
【解析】
(1)考慮元素1,2,結合新定義SA,可得所求值;
(2)從兩個方面證明,結合等差數列的性質和求和公式,即可得證;
(3)由于含有n個元素的非空子集個數有2n﹣1,討論當n=10時,n=11時,結合條件和新定義,推理可得所求.
(1)由條件知1≤SA,必有1∈A,又a1<a2<…<an均為整數,a1=1,
2≤SA,由SA的定義及a1<a2<…<an均為整數,必有2∈A,a2=2;
(2)證明:必要性:由“a1,a2,…,an成等差數列”及a1=1,a2=2,
得ai=i(i=1,2,…,n)此時A={1,2,3,…,n}滿足題目要求,
從而![]() ;
;
充分性:由條件知a1<a2<…<an,且均為正整數,可得ai≥i(i=1,2,3,…,n),
故![]() ,當且僅當ai=i(i=1,2,3,…,n)時,上式等號成立.
,當且僅當ai=i(i=1,2,3,…,n)時,上式等號成立.
于是當![]() 時,ai=i(i=1,2,3,…,n),從而a1,a2,…,an成等差數列.
時,ai=i(i=1,2,3,…,n),從而a1,a2,…,an成等差數列.
所以“a1,a2,…,an成等差數列”的充要條件是“![]() ”;
”;
(Ⅲ)由于含有n個元素的非空子集個數有2n-1,故當n=10時,210﹣1=1023,
此時A的非空子集的元素之和最多表示1023個不同的整數m,不符合要求.
而用11個元素的集合A={1,2,4,8,16,32,64,128,256,512,1024}的非空子集的元素之和
可以表示1,2,3,…,2046,2047共2047個正整數.
因此當SA=2020時,n的最小值為11.
記S10=a1+a2+…+a10,則S10+a11=2020并且S10+1≥a11.
事實上若S10+1<a11,2020=S10+a11<2a11,則a11>1010,S10<a11<1010,
所以m=1010時無法用集合A的非空子集的元素之和表示,與題意不符.
于是2020=S10+a11≥2a11﹣1,得![]() ,
,![]() ,所以a11≤1010.
,所以a11≤1010.
當a11=1010時,A={1,2,4,8,16,32,64,128,256,499,1010}滿足題意,
所以當SA=2020時,n的最小值為11,此時an的最大值1010.


科目:高中數學 來源: 題型:
【題目】現有四個函數①y=x|sinx|,②y=xcos|x|,③![]() ,④y=xln|x|的部分圖象如下,但順序被打亂,則按照圖象從左到右的順序,對應的函數序號正確的一組是( )
,④y=xln|x|的部分圖象如下,但順序被打亂,則按照圖象從左到右的順序,對應的函數序號正確的一組是( )
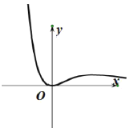
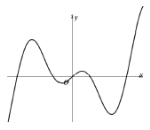
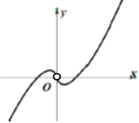
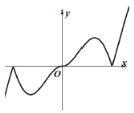
A.①④②③B.①④③②C.③②④①D.③④②①
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】田忌賽馬是《史記》中記載的一個故事,說的是齊國大將軍田忌經常與齊國眾公子賽馬,孫臏發現田忌的馬和其他人的馬相差并不遠,都分為上、中、下三等.于是孫臏給田忌將軍獻策:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得了許多賭注.假設田忌的各等級馬與某公子的各等級馬進行一場比賽,田忌獲勝的概率如下表所示:
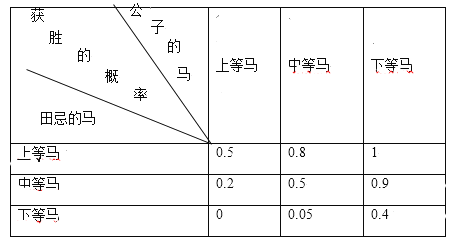
比賽規則規定:一次比賽由三場賽馬組成,每場由公子和田忌各出一匹馬參賽,結果只有勝和負兩種,并且毎一方三場賽馬的馬的等級各不相同,三場比賽中至少獲勝兩場的一方為最終勝利者.
(1)如果按孫臏的策略比賽一次,求田忌獲勝的概率;
(2)如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() ).
).
(Ⅰ)若![]() 是函數
是函數![]() 的一個極值點,求
的一個極值點,求![]() 的值;
的值;
(Ⅱ)求證:當![]() 時,
時,![]() 在
在![]() 上是增函數;
上是增函數;
(Ⅲ)若對任意的![]() (1,2),總存在
(1,2),總存在![]() ,使不等式
,使不等式![]() 成立,求實數
成立,求實數![]() 的取范圍.
的取范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓方程為![]() ,其右焦點
,其右焦點![]() 與拋物線
與拋物線![]() 的焦點重合,過
的焦點重合,過![]() 且垂直于拋物線對稱軸的直線與橢圓交于
且垂直于拋物線對稱軸的直線與橢圓交于![]() 、
、![]() 兩點,與拋物線交于
兩點,與拋物線交于![]() 、
、![]() 兩點.
兩點.![]()
(1)求橢圓的方程;
(2)若直線l與(1)中橢圓相交于![]() ,
,![]() 兩點, 直線
兩點, 直線![]() ,
, ![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() (其中
(其中![]() ),且
),且![]() ,
,![]() ,
,![]() 成等比數列;設
成等比數列;設![]() 的面積為
的面積為![]() , 以
, 以![]() 、
、![]() 為直徑的圓的面積分別為
為直徑的圓的面積分別為![]() ,
, ![]() , 求
, 求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() (任意項都不為零)的前
(任意項都不為零)的前![]() 項和為
項和為![]() ,首項為
,首項為![]() ,對于任意
,對于任意![]() ,滿足
,滿足![]() .
.
(1)數列![]() 的通項公式;
的通項公式;
(2)是否存在![]() 使得
使得![]() 成等比數列,且
成等比數列,且![]() 成等差數列?若存在,試求
成等差數列?若存在,試求![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(3)設數列![]() ,
, ,若由
,若由![]() 的前
的前![]() 項依次構成的數列是單調遞增數列,求正整數
項依次構成的數列是單調遞增數列,求正整數![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com