
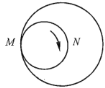
【題目】如圖,一個直徑為1的小圓沿著直徑為2的大圓內(nèi)壁的逆時針方向滾動,M和N是小圓的一條固定直徑的兩個端點,那么,當小圓這樣滾過大圓內(nèi)壁的一周,點M,N在大圓內(nèi)所繪出的圖形大致是( )
A.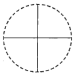 B.
B.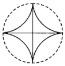 C.
C.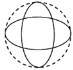 D.
D.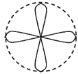
【答案】A
【解析】
設(shè)某時刻兩圓相切于點![]() ,此時動點
,此時動點![]() 所處的位置為點
所處的位置為點![]() ,以切點
,以切點![]() 在如圖上運動為例,記直線
在如圖上運動為例,記直線![]() 與此時小圓
與此時小圓![]() 的交點為
的交點為![]() ,利用弧長公式計算,可知小圓的圓弧
,利用弧長公式計算,可知小圓的圓弧![]() 與圓弧
與圓弧![]() 的長相等,可得點
的長相等,可得點![]() 與點
與點![]() 重合,即動點
重合,即動點![]() 在線段
在線段![]() 上運動,同理可知,此時點
上運動,同理可知,此時點![]() 在與
在與![]() 垂直的線段上運動,再通過觀察四個選項可得答案.
垂直的線段上運動,再通過觀察四個選項可得答案.
如圖所示:
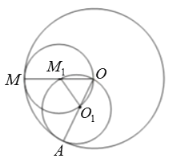
由題意可知,小圓![]() 總與大圓
總與大圓![]() 相內(nèi)切,且小圓
相內(nèi)切,且小圓![]() 總經(jīng)過大圓的圓心
總經(jīng)過大圓的圓心![]() ,
,
設(shè)某時刻兩圓相切于點![]() ,此時動點
,此時動點![]() 所處的位置為點
所處的位置為點![]() ,
,
則大圓圓弧![]() 與小圓
與小圓![]() 轉(zhuǎn)過的圓弧相等,
轉(zhuǎn)過的圓弧相等,
以切點![]() 在如圖上運動為例,記直線
在如圖上運動為例,記直線![]() 與此時小圓
與此時小圓![]() 的交點為
的交點為![]() ,
,
記![]() ,則
,則![]() ,
,
所以![]()
![]() ,
,
所以大圓圓弧![]() 的長為
的長為![]() ,小圓圓弧
,小圓圓弧![]() 的長為
的長為![]() ,
,
所以![]() ,
,
所以小圓的圓弧![]() 與圓弧
與圓弧![]() 的長相等,
的長相等,
所以點![]() 與點
與點![]() 重合,即動點
重合,即動點![]() 在線段
在線段![]() 上運動,
上運動,
同理可知,此時點![]() 在與
在與![]() 垂直的線段上運動,
垂直的線段上運動,
點![]() 在其它位置類似可得,
在其它位置類似可得,![]() 、
、![]() 的軌跡為互相垂直的線段.
的軌跡為互相垂直的線段.
觀察四個選項可知,只有選項![]() 符合.
符合.
故選:A.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數(shù)學 來源: 題型:
【題目】著名數(shù)學家華羅庚先生曾說過:“數(shù)缺形時少直觀,形缺數(shù)時難入微數(shù)形結(jié)合百般好,隔裂分家萬事休.”在數(shù)學的學習和研究中,我們經(jīng)常用函數(shù)的圖象來研究函數(shù)的性質(zhì),也經(jīng)常用函數(shù)的解析式來琢磨函數(shù)的圖象的特征,如某體育品牌的LOGO為![]() ,可抽象為如圖所示的軸對稱的優(yōu)美曲線,下列函數(shù)中,其圖象大致可“完美”局部表達這條曲線的函數(shù)是( )
,可抽象為如圖所示的軸對稱的優(yōu)美曲線,下列函數(shù)中,其圖象大致可“完美”局部表達這條曲線的函數(shù)是( )
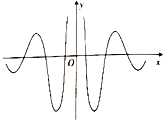
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=|x+1|﹣|2x﹣2|的最大值為M,正實數(shù)a,b滿足a+b=M.
(1)求2a2+b2的最小值;
(2)求證:aabb≥ab.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中e為自然對數(shù)的底數(shù).
,其中e為自然對數(shù)的底數(shù).
(1)若函數(shù)![]() 的圖象在點
的圖象在點![]() 處的切線方程為
處的切線方程為![]() ,求實數(shù)a的值;
,求實數(shù)a的值;
(2)若函數(shù)![]() 有2個不同的零點
有2個不同的零點![]() ,
,![]() .
.
①求實數(shù)a的取值范圍;
②求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨機調(diào)查某城市80名有子女在讀小學的成年人,以研究晚上八點至十點時間段輔導子女作業(yè)與性別的關(guān)系,得到下面的數(shù)據(jù)表:
是否輔導 性別 | 輔導 | 不輔導 | 合計 |
男 | 25 | 60 | |
女 | |||
合計 | 40 | 80 |
(1)請將表中數(shù)據(jù)補充完整;
(2)用樣本的頻率估計總體的概率,估計這個城市有子女在讀小學的成人女性晚上八點至十點輔導子女作業(yè)的概率;
(3)根據(jù)以上數(shù)據(jù),能否有99%以上的把握認為“晚上八點至十點時間段是否輔導子女作業(yè)與性別有關(guān)?”.
參考公式: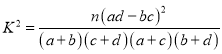 ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,動點![]() 到兩定點
到兩定點![]() 、
、![]() 構(gòu)成
構(gòu)成![]() ,且
,且![]() ,設(shè)動點
,設(shè)動點![]() 的軌跡為
的軌跡為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)設(shè)直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與軌跡
,與軌跡![]() 相交于點
相交于點![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)求 函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)定義:對于函數(shù)![]() ,若存在
,若存在![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為函數(shù)
為函數(shù)![]() 的不動點. 如果函數(shù)
的不動點. 如果函數(shù)![]() 存在兩個不同的不動點,求實數(shù)
存在兩個不同的不動點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為調(diào)查某公司五類機器的銷售情況,該公司隨機收集了一個月銷售的有關(guān)數(shù)據(jù),公司規(guī)定同一類機器銷售價格相同,經(jīng)分類整理得到下表:
機器類型 | 第一類 | 第二類 | 第三類 | 第四類 | 第五類 |
銷售總額(萬元) |
|
|
|
|
|
銷售量(臺) |
|
|
|
|
|
利潤率 |
|
|
|
|
|
利潤率是指:一臺機器銷售價格減去出廠價格得到的利潤與該機器銷售價格的比值.
(Ⅰ)從該公司本月賣出的機器中隨機選一臺,求這臺機器利潤率高于0.2的概率;
(Ⅱ)從該公司本月賣出的銷售單價為20萬元的機器中隨機選取![]() 臺,求這兩臺機器的利潤率不同的概率;
臺,求這兩臺機器的利潤率不同的概率;
(Ⅲ)假設(shè)每類機器利潤率不變,銷售一臺第一類機器獲利![]() 萬元,銷售一臺第二類機器獲利
萬元,銷售一臺第二類機器獲利![]() 萬元,…,銷售一臺第五類機器獲利
萬元,…,銷售一臺第五類機器獲利![]() ,依據(jù)上表統(tǒng)計數(shù)據(jù),隨機銷售一臺機器獲利的期望為
,依據(jù)上表統(tǒng)計數(shù)據(jù),隨機銷售一臺機器獲利的期望為![]() ,設(shè)
,設(shè)![]() ,試判斷
,試判斷![]() 與
與![]() 的大小.(結(jié)論不要求證明)
的大小.(結(jié)論不要求證明)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某省即將實行新高考,不再實行文理分科.某校為了研究數(shù)學成績優(yōu)秀是否對選擇物理有影響,對該校2018級的1000名學生進行調(diào)查,收集到相關(guān)數(shù)據(jù)如下:
(1)根據(jù)以上提供的信息,完成![]() 列聯(lián)表,并完善等高條形圖;
列聯(lián)表,并完善等高條形圖;
選物理 | 不選物理 | 總計 | |
數(shù)學成績優(yōu)秀 | |||
數(shù)學成績不優(yōu)秀 | 260 | ||
總計 | 600 | 1000 |
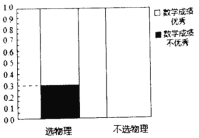
(2)能否在犯錯誤的概率不超過0.05的前提下認為數(shù)學成績優(yōu)秀與選物理有關(guān)?
附: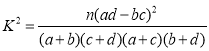
臨界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com