【題目】某地區2008年至2016年糧食產量的部分數據如下表：
（1）求該地區2008年至2016年的糧食年產量
與年份
之間的線性回歸方程；
（2）利用（1）中的回歸方程，分析2008年至2016年該地區糧食產量的變化情況，并預測該地區 2018年的糧食產量.
附:回歸直線的斜率和截距的最小二乘估計公式分別為
，
.
【答案】（1）
；（2）測該地區2018 量為299. 2萬噸.
【解析】試題分析：（1）計算
和
，利用
的計算公式即可得解；
（2）由的意義得該地區糧食產量逐年增加，平均每兩年增加6. 5 萬噸，將
代入中的線性回歸方程得預測值.
試題解析：
（1）由所給數據可以看出，糧食年產量
與年份
之間是近似直線上升，下面來求線性回歸方程，為此對數據預處理如下：
對預處理后的數據，容易算得
，
∴
，
.
由上述計算結果，知所求線性回歸方程為
，
即
.
（2）由（1)知，
，故2008年至2016年該地區糧食產量逐年增加，平均每兩年增加6. 5 萬噸.
將代入（1）中的線性回歸方程，得
，故預測該地區2018 量為299. 2萬噸.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】隨著人們對環境關注度的提高，綠色低碳出行越來越受到市民重視. 為此貴陽市建立了公共自行車服務系統，市民憑本人二代身份證到自行車服務中心辦理誠信借車卡借車，初次辦卡時卡內預先贈送20積分，當積分為0時，借車卡將自動鎖定，限制借車，用戶應持卡到公共自行車服務中心以1元購1個積分的形式再次激活該卡，為了鼓勵市民租用公共自行車出行，同時督促市民盡快還車，方便更多的市民使用，公共自行車按每車每次的租用時間進行扣分收費，具體扣分標準如下：
①租用時間不超過1小時，免費；
②租用時間為1小時以上且不超過2小時，扣1分；
③租用時間為2小時以上且不超過3小時，扣2分；
④租用時間超過3小時，按每小時扣2分收費（不足1小時的部分按1小時計算）.
甲、乙兩人獨立出行，各租用公共自行車一次，兩人租車時間都不會超過3小時，設甲、乙租用時間不超過1小時的概率分別是0.4和0.5；租用時間為1小時以上且不超過2小時的概率分別是0.4和0.3.
（1）求甲、乙兩人所扣積分相同的概率；
（2）設甲、乙兩人所扣積分之和為隨機變量
，求
的分布列和數學期望
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝|x－a|．
(1)若不等式f(x)≤3的解集為{x|－1≤x≤5}，求實數a的值；
(2)在(1)的條件下，若f(x)＋f(x＋5)≥m對一切實數x恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，矩形ABCD的邊AB=m，BC=4，PA⊥平面ABCD，PA=3，現有數據：
① 
；②m=3；③m=4；④ 
．若在BC邊上存在點Q（Q不在端點B、C處），使PQ⊥QD，則m可以取（ ）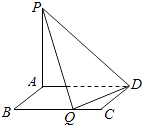
A.①②
B.①②③
C.②④
D.①
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設進入某商場的每一位顧客購買甲種商品的概率為0.5，購買乙種商品的概率為0.6，且購買甲種商品與購買乙種商品相互獨立，各顧客之間購買商品也是相互獨立的．
（1）求進入商場的1位顧客購買甲、乙兩種商品中的一種的概率；
（2）求進入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率；
（3）記ξ表示進入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數，求ξ的分布列及期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數y=f（x）是定義域為R的偶函數，當x≥0時，f（x）=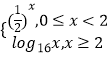 
，若關于x的方程[f（x）]2+af（x）﹣a﹣1=0（a∈R）有且只有7個不同實數根，則a的取值范圍是 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
