
【題目】甲、乙兩名同學準備參加考試,在正式考試之前進行了十次模擬測試,測試成績如下:
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)畫出甲、乙兩人成績的莖葉圖,求出甲同學成績的平均數和方差,并根據莖葉圖,寫出甲、乙兩位同學平均成績以及兩位同學成績的中位數的大小關系的結論;
(2)規定成績超過127為“良好”,現在老師分別從甲、乙兩人成績中各隨機選出一個,求選出成績“良好”的個數![]() 的分布列和數學期望.
的分布列和數學期望.
(注:方差![]() ,其中
,其中![]() 為
為![]() 的平均數)
的平均數)
【答案】(1)![]() ,甲的中位數大于乙的中位數,甲的平均成績小于乙的平均成績
,甲的中位數大于乙的中位數,甲的平均成績小于乙的平均成績
(2)![]()
【解析】試題分析:(1)根據根據所給數據,利用莖葉圖的作法可得莖葉圖,根據莖葉圖可得甲乙兩人成績的中位數,根據平均值公式可得甲乙兩人的平均成績![]() 根據方差公式可得甲的方程
根據方差公式可得甲的方程![]() ,比較兩人的成績的中位數及平均成績即可的結果;(2)
,比較兩人的成績的中位數及平均成績即可的結果;(2)![]() 的可能取值為0,1,2,分別求出各隨機變量對應的概率,從而可得分布列,進而利用期望公式可得
的可能取值為0,1,2,分別求出各隨機變量對應的概率,從而可得分布列,進而利用期望公式可得![]() 的數學期望..
的數學期望..
試題解析:(1)莖葉圖如圖
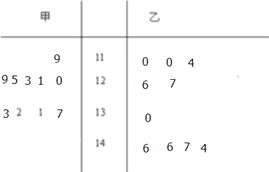
乙的均值為![]() ,中位數為
,中位數為![]() ;甲的平均值為
;甲的平均值為![]() ,中位數為
,中位數為![]() ,甲的方差為
,甲的方差為![]() ,所以甲的中位數大于乙的中位數,甲的平均成績小于乙的平均成績 ;
,所以甲的中位數大于乙的中位數,甲的平均成績小于乙的平均成績 ;
(2)由已知, ![]() 的可能取值為0,1,2,
的可能取值為0,1,2,
分布列為:
| 0 | 1 | 2 |
|
|
|
|
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.


科目:高中數學 來源: 題型:
【題目】2017年5月14日至15日,“一帶一路”國際合作高峰論壇在中國首都北京舉行,會議期間,達成了多項國際合作協議.假設甲、乙兩種品牌的同類產品出口某國家的市場銷售量相等,該國質量檢驗部門為了解他們的使用壽命,現從這兩種品牌的產品中分別隨機抽取300個進行測試,結果統計如下圖所示,已知乙品牌產品使用壽命小于200小時的概率估計值為![]() .
.
(1)求![]() 的值;
的值;
(2)估計甲品牌產品壽命小于200小時的概率;
(3)這兩種品牌產品中,某個產品已使用了200小時,試估計該產品是乙品牌的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是( )
A. 命題“若![]() ,則
,則![]() ”的逆否命題為“若
”的逆否命題為“若![]() ,則
,則![]() ”
”
B. 若命題![]() “
“![]() ,
, ![]() ”,則命題
”,則命題![]() 的否定為“
的否定為“![]() ,
, ![]() ”
”
C. “![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
D. “![]() ”是“直線
”是“直線![]() 與直線
與直線![]() 互為垂直”的充要條件
互為垂直”的充要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據某市地產數據研究的數據顯示,2016年該市新建住宅銷售均價走勢如下圖所示,為抑制房價過快上漲,政府從8月采取宏觀調控措施,10月份開始房價得到很好的抑制.
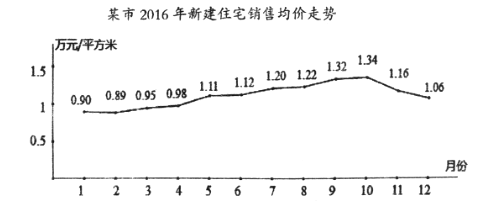
(1)地產數據研究院發現,3月至7月的各月均價![]() (萬元/平方米)與月份
(萬元/平方米)與月份![]() 之間具有較強的線性相關關系,試建立
之間具有較強的線性相關關系,試建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01);政府若不調控,依此相關關系預測第12月份該市新建住宅銷售均價;
的回歸方程(系數精確到0.01);政府若不調控,依此相關關系預測第12月份該市新建住宅銷售均價;
(2)地產數據研究院在2016年的12個月份中,隨機抽取三個月的數據作樣本分析,若關注所抽三個月份的所屬季度,記不同季度的個數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考數據: ![]() ,
, ![]() ,
, ![]() ;
;
回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為:
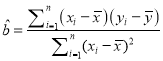 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,值域為
,值域為![]() ,即
,即![]() ,若
,若![]() ,則稱
,則稱![]() 在
在![]() 上封閉.
上封閉.
(1)分別判斷函數![]() ,
, ![]() 在
在![]() 上是否封閉,說明理由;
上是否封閉,說明理由;
(2)函數![]() 的定義域為
的定義域為![]() ,且存在反函數
,且存在反函數![]() ,若函數
,若函數![]() 在
在![]() 上封閉,且函數
上封閉,且函數![]() 在
在![]() 上也封閉,求實數
上也封閉,求實數![]() 的取值范圍;
的取值范圍;
(3)已知函數![]() 的定義域為
的定義域為![]() ,對任意
,對任意![]() ,若
,若![]() ,有
,有![]() 恒成立,則稱
恒成立,則稱![]() 在
在![]() 上是單射,已知函數
上是單射,已知函數![]() 在
在![]() 上封閉且單射,并且滿足
上封閉且單射,并且滿足![]()
![]() ,其中
,其中![]() (
(![]() ),
),![]() ,證明:存在
,證明:存在![]() 的真子集,
的真子集, ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,使得
,使得![]() 在所有
在所有![]() (
(![]() )上封閉.
)上封閉.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:只要
滿足:只要![]() ,必有
,必有![]() ,則稱
,則稱![]() 具有性質
具有性質![]() .
.
(1)若![]() 具有性質
具有性質![]() ,且
,且![]() ,
, ![]() ,求
,求![]() ;
;
(2)若無窮數列![]() 是等差數列,無窮數列
是等差數列,無窮數列![]() 是公比為正數的等比數列,
是公比為正數的等比數列, ![]() ,
, ![]() ,
, ![]() 判斷
判斷![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(3)設![]() 是無窮數列,已知
是無窮數列,已知![]() .求證:“對任意
.求證:“對任意![]() 都具有性質
都具有性質![]() ”的充要條件為“
”的充要條件為“![]() 是常數列”.
是常數列”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com