Question

【題目】設是定義在上的函數(shù)，若存在，使得在單調遞增，在上單調遞減，則稱為上的單峰函數(shù)，為峰點，包含峰點的區(qū)間稱為含峰區(qū)間，其含峰區(qū)間的長度為：．

（1）判斷下列函數(shù)中，哪些是“上的單峰函數(shù)”？若是，指出峰點；若不是，說出原因；；

（2）若函數(shù)是上的單峰函數(shù)，求實數(shù)的取值范圍；

（3）若函數(shù)是區(qū)間上的單峰函數(shù)，證明：對于任意的，若，則為含峰區(qū)間；若，則為含峰區(qū)間；試問當滿足何種條件時，所確定的含峰區(qū)間的長度不大于0.6．

Answer 1

【答案】（1）見解析（2）（3）證明見解析；

【解析】

（1）畫出四個函數(shù)圖像，根據(jù)圖像集合單峰函數(shù)的定義進行判斷.

（2）利用的導函數(shù)的零點在區(qū)間列不等式，解不等式求得的取值范圍.

（3）分成、兩種情況進行分類討論，利用反證法證得結論成立.根據(jù)含峰區(qū)間的長度的概念列不等式，由此確定滿足的條件.

（1）①圖像如下圖所示，其對稱軸為，由圖可知，是上的單峰函數(shù)，峰點為；

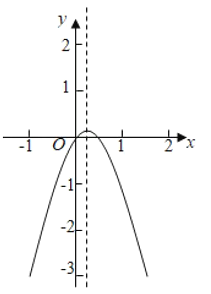
②的圖像如下圖所示，其對稱軸為，由圖可知，是上的單峰函數(shù)，峰點為；

③的圖像如下圖所示，根據(jù)圖像可知，不是上的單峰函數(shù)；

④的圖像如下圖所示，其對稱軸為，由圖可知，是上的單峰函數(shù)，峰點為.

（2）函數(shù)是上的單峰函數(shù)，令，解得，故時，遞增，時，遞減，所以，解得，故的取值范圍是.

（3）設為的峰點，則由單峰函數(shù)定義可知，在上遞增，在上遞減.

當時，假設，則，從而，與矛盾，所以，即是含峰區(qū)間.

當時，假設，則，從而，與矛盾，所以，即是含峰區(qū)間.

在所得的含峰區(qū)間內選取，由與或與，確定一個新的含峰區(qū)間，對先選擇的，，①，在第一次確定的含峰區(qū)間為的情況下，的取值應滿足②，由①②可得，當時，含峰區(qū)間的長度為.

由條件，得，從而.因此確定的含峰區(qū)間的長度不大于，只要取.