
(2)已知雙曲線的焦點在y軸上,并且雙曲線上兩點P1、P2的坐標分別為(3,-4![]() )、(
)、(![]() ,5),求雙曲線的標準方程.
,5),求雙曲線的標準方程.
分析:
第(1)題由橢圓的方程確定焦點坐標,可求得c值,設雙曲線方程為![]() (a>0,b>0),用待定系數法,求得a、b;第(2)題可先設出標準方程,然后把P1、P2點坐標代入方程,聯立方程組,求a2、b2的值.
(a>0,b>0),用待定系數法,求得a、b;第(2)題可先設出標準方程,然后把P1、P2點坐標代入方程,聯立方程組,求a2、b2的值.
解:(1)橢圓![]() 的焦點為(2
的焦點為(2![]() ,0),(-2
,0),(-2![]() ,0),
,0),
設雙曲線的方程為![]() ,則a2+b2=20.
,則a2+b2=20.
又∵過點(3![]() ,
,![]() ),
),
∴![]()
綜上,得a2=20-2![]() ,b2=2
,b2=2![]() ,
,
∴雙曲線方程為![]()
(2)∵雙曲線的焦點在y軸上,
∴設雙曲線的標準方程為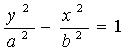 (a>0,b>0), ①
(a>0,b>0), ①
∵點P1、P2在雙曲線上,
∴點P1、P2的坐標適合方程①.
將(3,-4![]() ),(
),(![]() ,5)分別代入方程①中,得方程組
,5)分別代入方程①中,得方程組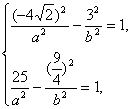
將![]() 看作整體,解得
看作整體,解得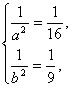
∴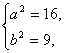 即雙曲線的標準方程為
即雙曲線的標準方程為![]()
綠色通道:本題只要解得a2、b2即可得到雙曲線的方程,不必求出a、b的值;在求解的過程中也可以用換元思想.


 活力試卷系列答案
活力試卷系列答案 課課優能力培優100分系列答案
課課優能力培優100分系列答案科目:高中數學 來源:2012-2013學年云南省昆明三中、滇池中學高二(上)期中數學試卷(理科)(解析版) 題型:解答題
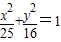 共焦點的拋物線的標準方程.
共焦點的拋物線的標準方程.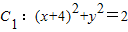 ,
,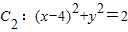 ,動圓M與兩圓一個內切,一個外切,求動圓圓心M的軌跡方程.
,動圓M與兩圓一個內切,一個外切,求動圓圓心M的軌跡方程.查看答案和解析>>
科目:高中數學 來源:2012-2013學年云南省昆明三中高二(上)期中數學試卷(文科)(解析版) 題型:解答題
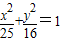 共焦點的拋物線的標準方程.
共焦點的拋物線的標準方程.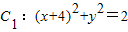 ,
,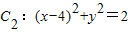 ,動圓M與兩圓一個內切,一個外切,求動圓圓心M的軌跡方程.
,動圓M與兩圓一個內切,一個外切,求動圓圓心M的軌跡方程.查看答案和解析>>
科目:高中數學 來源:2012-2013學年云南省昆明三中高二(上)期中數學試卷(理科)(解析版) 題型:解答題
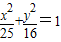 共焦點的拋物線的標準方程.
共焦點的拋物線的標準方程.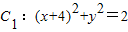 ,
,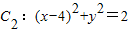 ,動圓M與兩圓一個內切,一個外切,求動圓圓心M的軌跡方程.
,動圓M與兩圓一個內切,一個外切,求動圓圓心M的軌跡方程.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com