
【題目】如圖1,在矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上,
上,![]() .把
.把![]() 沿
沿![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,連結
,連結![]() ,點
,點![]() 在線段
在線段![]() 上,
上,![]() ,如圖2.
,如圖2.

(1)證明:![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 的體積最大時,求二面角
的體積最大時,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)依題意得,可得出![]() ,
,![]() ,在線段
,在線段![]() 上取一點
上取一點![]() ,滿足
,滿足![]() ,可求出
,可求出![]() ,結合
,結合![]() 得出
得出![]() ,從而可證出四邊形
,從而可證出四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,再利用線面平行的判定定理,即可證出
,再利用線面平行的判定定理,即可證出![]() 平面
平面![]() ;
;
(2)設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,三棱錐
,三棱錐![]() 的體積最大時,即
的體積最大時,即![]() 取到最大值,從而得出當平面
取到最大值,從而得出當平面![]() 平面
平面![]() 時,
時,![]() 取得最大值,此時
取得最大值,此時![]() ,建立空間直角坐標系,利用向量法分別求出平面
,建立空間直角坐標系,利用向量法分別求出平面![]() 和平面
和平面![]() 的法向量,運用向量法求二面角的公式,即可得出二面角
的法向量,運用向量法求二面角的公式,即可得出二面角![]() 的余弦值.
的余弦值.
(1)依題意得,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
在線段![]() 上取一點
上取一點![]() ,滿足
,滿足![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
故![]() ,
,
又因為![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() ,
,
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.

(2)設![]() 到平面
到平面![]() 的距離為
的距離為![]() ,
,![]() ,又
,又![]() ,
,
所以![]() ,故要使三棱錐
,故要使三棱錐![]() 的體積取到最大值,僅需
的體積取到最大值,僅需![]() 取到最大值.
取到最大值.
取![]() 的中點
的中點![]() ,連結
,連結![]() ,依題意得
,依題意得![]() ,則
,則![]() ,
,
因為平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
故當平面![]() 平面
平面![]() 時,
時,![]() 平面
平面![]() ,
,![]() .
.
即當且僅當平面![]() 平面
平面![]() 時,
時,![]() 取得最大值,此時
取得最大值,此時![]() .
.
如圖,以![]() 為坐標原點,
為坐標原點,![]() ,
,![]() 的方向分別為
的方向分別為![]() 軸,
軸,![]() 軸的正方向建立空間直角坐
軸的正方向建立空間直角坐
標系![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,

設![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
則
得 令
令![]() ,解得
,解得![]() ,
,
又因為平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以 ,
,
因為![]() 為鈍角,所以其余弦值等于
為鈍角,所以其余弦值等于![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
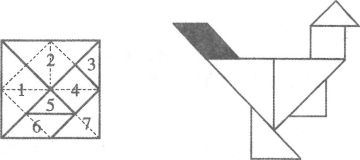
【題目】七巧板是一種古老的中國傳統智力玩具,是由七塊板組成的.而這七塊板可拼成許多圖形,例如:三角形、不規則多邊形、各種人物、動物、建筑物等,清陸以湉《冷廬雜識》寫道:近又有七巧圖,其式五,其數七,其變化之式多至千余.在18世紀,七巧板流傳到了國外,至今英國劍橋大學的圖書館里還珍藏著一部《七巧新譜》.若用七巧板拼成一只雄雞,在雄雞平面圖形上隨機取一點,則恰好取自雄雞雞尾(陰影部分)的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學參加詩詞大賽,各答3道題,每人答對每道題的概率均為![]() ,且各人是否答對每道題互不影響.
,且各人是否答對每道題互不影響.
(Ⅰ)用![]() 表示甲同學答對題目的個數,求隨機變量
表示甲同學答對題目的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)設![]() 為事件“甲比乙答對題目數恰好多2”,求事件
為事件“甲比乙答對題目數恰好多2”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐D-ABC中,![]() ,且
,且![]() ,
,![]() ,M,N分別是棱BC,CD的中點,下面結論正確的是( )
,M,N分別是棱BC,CD的中點,下面結論正確的是( )
A.![]() B.
B.![]() 平面ABD
平面ABD
C.三棱錐A-CMN的體積的最大值為![]() D.AD與BC一定不垂直
D.AD與BC一定不垂直
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐D-ABC中,![]() ,且
,且![]() ,
,![]() ,M,N分別是棱BC,CD的中點,下面結論正確的是( )
,M,N分別是棱BC,CD的中點,下面結論正確的是( )
A.![]() B.
B.![]() 平面ABD
平面ABD
C.三棱錐A-CMN的體積的最大值為![]() D.AD與BC一定不垂直
D.AD與BC一定不垂直
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com