
【題目】拋物線y=(x﹣3)(x+1)與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點.

(1)求點B及點D的坐標.
(2)連結BD,CD,拋物線的對稱軸與x軸交于點E.
①若線段BD上一點P,使∠DCP=∠BDE,求點P的坐標.
②若拋物線上一點M,作MN⊥CD,交直線CD于點N,使∠CMN=∠BDE,求點M的坐標.
【答案】(1)(1,﹣4);(2)點M坐標為(![]() ,﹣
,﹣![]() )或(5,12).
)或(5,12).
【解析】試題分析:(1)解方程![]() 求出
求出![]() 或
或![]() 拋物線
拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點A在點B左側),確定點
兩點(點A在點B左側),確定點![]() 的坐標為
的坐標為![]() 將
將![]() 配方,寫成頂點式為
配方,寫成頂點式為![]() 即可確定頂點
即可確定頂點![]() 的坐標;
的坐標;
(2)①根據拋物線![]() 得到點C、點E的坐標.連接BC,過點C作
得到點C、點E的坐標.連接BC,過點C作![]() 于H,由勾股定理得出
于H,由勾股定理得出![]() 證明
證明![]() 為直角三角形.
為直角三角形.
分別延長![]() 與
與![]() 軸相交于點
軸相交于點![]() 根據兩角對應相等的兩三角形相似證明
根據兩角對應相等的兩三角形相似證明![]()
![]() 得出
得出![]() 運用待定系數(shù)法求出直線CQ的解析式為
運用待定系數(shù)法求出直線CQ的解析式為![]() y=-直線BD的解析式為
y=-直線BD的解析式為![]() 解方程組
解方程組 即可求出點P的坐標;
即可求出點P的坐標;
②分兩種情況進行討論:(Ⅰ)當點M在對稱軸右側時.若點N在射線CD上,如備用圖1,延長MN交y軸于點F,過點M作![]() 軸于點G,先證明
軸于點G,先證明![]() 由相似三角形對應邊成比例得出
由相似三角形對應邊成比例得出![]() .設
.設![]() ,再證明
,再證明![]() 均為等腰直角三角形,然后用含
均為等腰直角三角形,然后用含![]() 的代數(shù)式表示點M的坐標,將其代入拋物線
的代數(shù)式表示點M的坐標,將其代入拋物線![]() 求出
求出![]() 的值,得到點M的坐標;若點N在射線DC上,同理可求出點M的坐標;(Ⅱ)當點M在對稱軸左側時.由于
的值,得到點M的坐標;若點N在射線DC上,同理可求出點M的坐標;(Ⅱ)當點M在對稱軸左側時.由于![]() 得到
得到![]() 根據直角三角形兩銳角互余得出
根據直角三角形兩銳角互余得出![]() 而拋物線左側任意一點K,都有
而拋物線左側任意一點K,都有![]() 所以點M不存在.
所以點M不存在.
試題解析:
(1)∵拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點A在點B左側),
兩點(點A在點B左側),
∴當![]() 時,
時,
![]()
解得![]() 或
或![]()
∴點B的坐標為![]()
![]()
∴頂點D的坐標為![]()
(2)①如右圖.
∵拋物線![]() 與與y軸交于點C,
與與y軸交于點C,
∴C點坐標為![]()
∵對稱軸為直線![]()
∴點E的坐標為![]()
連接BC,過點C作![]() 于H,則H點坐標為
于H,則H點坐標為![]()
![]()
![]()
![]()
![]() 為直角三角形.
為直角三角形.
分別延長![]() 與
與![]() 軸相交于點
軸相交于點![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 即
即![]()
∴直線CQ的解析式為![]()
直線BD的解析式為![]()
由方程組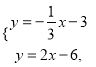 解得
解得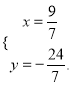 .
.
∴點P的坐標為![]()
②(Ⅰ)當點M在對稱軸右側時.
若點![]() 在射線
在射線![]() 上,如備用圖1,延長MN交
上,如備用圖1,延長MN交![]() 軸于點F,過點M作
軸于點F,過點M作![]() 軸于點
軸于點![]() .
.
![]()
![]()
![]()
![]()
設![]() 則
則![]()
![]()
![]() 均為等腰直角三角形,
均為等腰直角三角形,
![]()
![]()
![]()
![]()
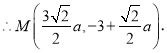
代入拋物線![]() 解得
解得![]()
![]()
若點N在射線DC上,如備用圖2,MN交y軸于點F,過點M作![]() 軸于點G.
軸于點G.
![]()
![]()
![]()
![]()
設![]() 則
則![]()
![]()
![]() 均為等腰直角三角形,
均為等腰直角三角形,
![]()
![]()
![]()
![]()
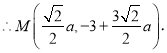
代入拋物線![]() 解得
解得![]()
代入拋物線![]() ,解得
,解得![]()
![]()
(Ⅱ)當點M在對稱軸左側時.
![]()
![]()
而拋物線左側任意一點K,都有![]()
∴點M不存在.
綜上可知,點M坐標為![]() 或
或![]()


 新題型全程檢測期末沖刺100分系列答案
新題型全程檢測期末沖刺100分系列答案科目:初中數(shù)學 來源: 題型:
【題目】平面直角坐標系中,我們把橫坐標、縱坐標都是整數(shù)的點稱為整點![]() 如圖,直線
如圖,直線![]() 和反比例函數(shù)
和反比例函數(shù)![]() 的圖象交于
的圖象交于![]() 兩點,則落在圖中陰影部分
兩點,則落在圖中陰影部分![]() 不包含邊界
不包含邊界![]() 內的整點個數(shù)有
內的整點個數(shù)有![]() 個.
個.

A. 2
B. 3
C. 4
D. 5
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)y=ax2+bx+c(a≠0)的圖象如圖所示,在下列五個結論中: ①abc<0;②4ac﹣b2>0;③a﹣b+c>2;④a<b<0;⑤ac+2=b,
正確的個數(shù)有________.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】把下列各數(shù)填入它所屬的集合內:5.2,0,![]() ,
,![]() ,+(﹣4),﹣2
,+(﹣4),﹣2![]() ,﹣(﹣3 ),0.25555…,﹣0.030030003…
,﹣(﹣3 ),0.25555…,﹣0.030030003…
(1)分數(shù)集合:{_________________________________________ …}
(2)非負整數(shù)集合:{_________________________________________ …}
(3)有理數(shù)集合:{_________________________________________…}.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】動點A從原點出發(fā)向數(shù)軸負方向運動,同時,動點B也從原點出發(fā)向數(shù)軸正方向運動,運動到3秒鐘時,兩點相距15個單位長度.已知動點A、B的運動速度比之是3:2(速度單位:1個單位長度/秒).
(1)求兩個動點運動的速度;
(2)A、B兩點運動到3秒時停止運動,請在數(shù)軸上標出此時A、B兩點的位置;
(3)若A、B兩點分別從(2)中標出的位置再次同時開始在數(shù)軸上運動,運動的速度不變,運動的方向不限,問:經過幾秒鐘,A、B兩點之間相距4個單位長度?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下列材料:
解方程:x4﹣6x2+5=0.這是一個一元四次方程,根據該方程的特點,它的解法通常是:
設x2=y,那么x4=y2,于是原方程可變?yōu)?/span>y2﹣6y+5=0…①,
解這個方程得:y1=1,y2=5.
當y=1時,x2=1,∴x=±1;
當y=5時,x2=5,∴x=±![]()
所以原方程有四個根:x1=1,x2=﹣1,x3=![]() ,x4=﹣
,x4=﹣![]() .
.
在這個過程中,我們利用換元法達到降次的目的,體現(xiàn)了轉化的數(shù)學思想.
(1)解方程(x2﹣x)2﹣4(x2﹣x)﹣12=0時,若設y=x2﹣x,則原方程可轉化為 ;求出x
(2)利用換元法解方程:![]() =2.
=2.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】線段AB和線段CD交于點O,OE平分∠AOC,點F為線段AB上一點(不與點A和點O重合)過點F作 FG//OE,交線段CD于點G,若∠AOD=110°,則∠AFG的度數(shù)為_____°.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我國![]() 道路交通安全法
道路交通安全法![]() 第四十七條規(guī)定“機動車行經人行橫道時,應當減速行駛;遇行人通過人行橫道,應當停車讓行”
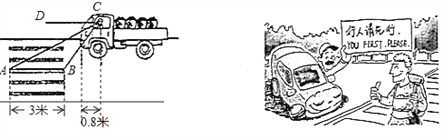
第四十七條規(guī)定“機動車行經人行橫道時,應當減速行駛;遇行人通過人行橫道,應當停車讓行” ![]() 如圖:一輛汽車在一個十字路口遇到行人時剎車停下,汽車里的駕駛員看地面的斑馬線前后兩端的視角分別是
如圖:一輛汽車在一個十字路口遇到行人時剎車停下,汽車里的駕駛員看地面的斑馬線前后兩端的視角分別是![]() 和
和![]() ,如果斑馬線的寬度是
,如果斑馬線的寬度是![]() 米,駕駛員與車頭的距離是
米,駕駛員與車頭的距離是![]() 米,這時汽車車頭與斑馬線的距離x是多少?
米,這時汽車車頭與斑馬線的距離x是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:如圖一次函數(shù)y1=-x-2與y2=x-4的圖象相交于點A.
(1)求點A的坐標;
(2)若一次函數(shù)y1=-x-2與y2=x-4的圖象與x軸分別相交于點B、C,求△ABC的面積.
(3)結合圖象,直接寫出y1>y2時x的取值范圍.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com