
【題目】如圖,在△ABC中,點D、E分別是邊BC、AC的中點,過點A作AF∥BC交DE的延長線于點F,連接CF。
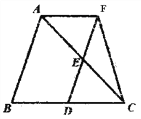
(1)求證:四邊形ABDF是平行四邊形;
(2)若∠CAF=45°,BC=4,CF=![]() ,求AB的長。
,求AB的長。
【答案】(1)證明見解析;
(2)AB的長為![]()
【解析】分析:(1)求出DE∥AB,AF∥BC來證明四邊形ABDF是平行四邊形.
(2)過點F作FG⊥AC于G點,求出AC和GF的長再求△CAF的面積.
本題解析:
證明:(1)在△ABC中,點D、E分別是邊BC、AC的中點,
∴DE∥AB, 又知AF∥BC,∴四邊形ABDF是平行四邊形。
(2)過點F作FG交AC于點G,過點A作AH交BC于點H。
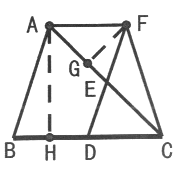
∵FG⊥AC,∴∠AGF=90°,∵∠CAF=45°,由(1)知,四邊形ABDF是平行四邊形,
∴AF=BD=![]() BC=2,在RT△AFG中,∠CAF=45°,∴AG=GF=
BC=2,在RT△AFG中,∠CAF=45°,∴AG=GF=![]() AF=
AF=![]() 。在RT△CFG中,CF=
。在RT△CFG中,CF=![]() ,
,
∴CG=![]() ,∵AF∥BC,∴∠ACB=45°,
,∵AF∥BC,∴∠ACB=45°,
∵AH⊥BC,在RT△ACH中,AC=AG+GC=![]() +2
+2![]() =3
=3![]() ,∴AH=HC=
,∴AH=HC=![]() ×3
×3![]() =3,
=3,
∴BH=BC-CH=4-3=1。在RT△ABH中,AB=![]() .
.


科目:初中數學 來源: 題型:
【題目】用三個正多邊形鑲嵌成一個平面時,若前兩種是正方形和正六邊形,則第三種是( )
A. 正十二邊形 B. 正十邊形 C. 正八邊形 D. 正三角形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a=3.1×10﹣4,b=5.2×10﹣8,判斷下列關于a﹣b之值的敘述何者正確?( )
A. 比1大 B. 介于0、1之間 C. 介于﹣1、0之間 D. 比﹣1小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:
第1個等式: ![]() ;
;
第2個等式: ![]() ;
;
第3個等式: ![]() ;
;
第4個等式: ![]() ;
;
…
請解答下列問題:
(1)按以上規律列出第6個等式: ![]() =_________=___________.
=_________=___________.
(2)用含有![]() 的代數式表示第
的代數式表示第![]() 個等式:
個等式: ![]() =__________=______________.
=__________=______________.
(![]() 為正整數);
為正整數);
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
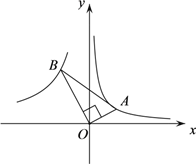
【題目】如圖,點A是反比例函數![]() 上的一個動點,連接OA,過點O作OB⊥OA,并且使OB=2OA,連接AB,當點A在反比函數圖象上移動時,點B也在某一反比例函數圖象
上的一個動點,連接OA,過點O作OB⊥OA,并且使OB=2OA,連接AB,當點A在反比函數圖象上移動時,點B也在某一反比例函數圖象![]() 上移動,
上移動, ![]() 的值為( )
的值為( )
A. 2 B. -2 C. 4 D. -4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數![]() (b為常數)的圖象與x軸交于點A(2,0),與y軸交于點B,與反比例函數
(b為常數)的圖象與x軸交于點A(2,0),與y軸交于點B,與反比例函數![]() 的圖象交于點C(-2,m).
的圖象交于點C(-2,m).
(1)求點C的坐標及反比例函數的表達式;
(2)過點C的直線與y軸交于點D,且![]() ,求點D的坐標.
,求點D的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com