Question

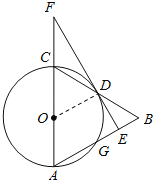
【題目】如圖，在△ABC中，以AC為直徑作⊙O交BC于點D，交AB于點G，且D是BC中點，DE⊥AB，垂足為E，交AC的延長線于點F．

（1）求證：直線EF是⊙O的切線；

（2）若CF=3，cosA=0.4，求出⊙O的半徑和BE的長；

（3）連接CG，在（2）的條件下，求CG:EF的值．

Answer 1

【答案】(1)見解析；（2）2， （3）CG:EF＝4：7

【解析】試題分析：（1）連結OD．先證明OD是△ABC的中位線，根據中位線的性質得到OD∥AB，再由DE⊥AB，得出OD⊥EF，根據切線的判定即可得出直線EF是⊙O的切線；

（2）先由OD∥AB，得出∠COD=∠A，再解Rt△DOF，根據余弦函數的定義得到cos∠FOD==，設⊙O的半徑為R，解方程=，求出R=，那么AB=2OD=，解Rt△AEF，根據余弦函數的定義得到cosA==，求出AE=，然后由BE=AB﹣AE即可求解．

試題解析：

（1）證明：如圖，連結OD．

∵CD=DB，CO=OA，

∴OD是△ABC的中位線，

∴OD∥AB，AB=2OD，

∵DE⊥AB，

∴DE⊥OD，即OD⊥EF，

∴直線EF是⊙O的切線；

（2）解：∵OD∥AB，

∴∠COD=∠A．

在Rt△DOF中，∵∠ODF=90°，

∴cos∠FOD==，

設⊙O的半徑為R，則=，

解得R=，

∴AB=2OD=．

在Rt△AEF中，∵∠AEF=90°，

∴cosA===，

∴AE=，

∴BE=AB﹣AE=﹣=2．