
【題目】綜合與探究
(實踐操作)三角尺中的數學
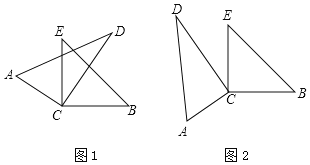
數學實踐活動課上,“奮進”小組將一副直角三角尺的直角頂點疊放在一起,如圖1,使直角頂點重合于點C.
(問題發現)
(1)①填空:如圖1,若∠ACB=145°,則∠ACE的度數是 ,∠DCB的度數 ,∠ECD的度數是 .
②如圖1,你發現∠ACE與∠DCB的大小有何關系?∠ACB與∠ECD的大小又有何關系?請直接寫出你發現的結論.
(類比探究)
(2)如圖2,當△ACD與△BCE沒有重合部分時,上述②中你發現的結論是否還依然成立?請說明理由.
【答案】(1)①55°, 55°, 35°;②∠ACE=∠DCB,∠ACB+∠ECD=180°;(2)當△ACD與△BCE沒有重合部分時,上述②中發現的結論依然成立,理由詳見解析
【解析】
(1)先計算出![]() ,再根據
,再根據![]() 即可求解;
即可求解;
(2)根據余角的性質可得![]() ,根據角的和差關系可得
,根據角的和差關系可得![]() ;
;
(3)利用周角定義得![]() ,而
,而![]() ,即可得到
,即可得到![]() .
.
解:(1)①![]() ,
,
![]() ;
;
②結論:![]() ,
,![]() ;
;
證明:∵![]() ,
,![]()
∴![]()
∵![]()
∴![]()
(2)結論:當![]() 與
與![]() 沒有重合部分時,上述②中發現的結論依然成立.
沒有重合部分時,上述②中發現的結論依然成立.
理由:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∴上述②中發現的結論依然成立.
故答案為:(1)①55°, 55°, 35°;②∠ACE=∠DCB,∠ACB+∠ECD=180°;(2)當△ACD與△BCE沒有重合部分時,上述②中發現的結論依然成立,理由詳見解析


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】程大位是我國明朝商人,珠算發明家.他60歲時完成的《直指算法統宗》是東方古代數學名著,詳述了傳統的珠算規則,確立了算盤用法.書中有如下問題:
一百饅頭一百僧,大僧三個更無爭,
小僧三人分一個,大小和尚得幾丁.
意思是:有100個和尚分100個饅頭,如果大和尚1人分3個,小和尚3人分1個,正好分完,大、小和尚各有多少人,下列求解結果正確的是( )

A. 大和尚25人,小和尚75人 B. 大和尚75人,小和尚25人
C. 大和尚50人,小和尚50人 D. 大、小和尚各100人
查看答案和解析>>
科目:初中數學 來源: 題型:
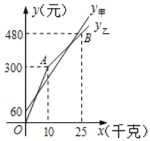
【題目】張莊甲、乙兩家草莓采摘園的草莓銷售價格相同,“春節期間”,兩家采摘園將推出優惠方案,甲園的優惠方案是:游客進園需購買門票,采摘的草莓六折優惠;乙園的優惠方案是:游客進園不需購買門票,采摘園的草莓超過一定數量后,超過部分打折優惠.優惠期間,某游客的草莓采摘量為![]() (千克),在甲園所需總費用為y甲(元),在乙園所需總費用為y乙(元),y甲、y乙與
(千克),在甲園所需總費用為y甲(元),在乙園所需總費用為y乙(元),y甲、y乙與![]() 之間的函數關系如圖所示,折線OAB表示y乙與
之間的函數關系如圖所示,折線OAB表示y乙與![]() 之間的函數關系.
之間的函數關系.
(1)甲采摘園的門票是 元,在乙園采摘草莓超過______![]() 后超過部分有打折優惠;
后超過部分有打折優惠;
(2)當采摘量![]() 時,采摘多少千克草莓,甲、乙兩家采摘園的總費用相同.
時,采摘多少千克草莓,甲、乙兩家采摘園的總費用相同.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,點D,E分別在邊AC,AB上,BD與CE交于點O,給出下列三個條件:①∠EBO=∠DCO;②
中,點D,E分別在邊AC,AB上,BD與CE交于點O,給出下列三個條件:①∠EBO=∠DCO;②![]() ;③
;③![]() .
.
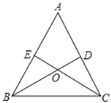
(1)上述三個條件中,由哪兩個條件可以判定![]() 是等腰三角形?(用序號寫出所有成立的情形)
是等腰三角形?(用序號寫出所有成立的情形)
(2)請選擇(1)中的一種情形,說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
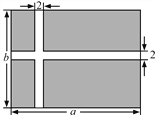
【題目】 某公園準備修建一塊長方形草坪,長為a米,寬為b米.并在草坪上修建如圖所示的十字路,
已知十字路寬2米.
(1)用含a、b的代數式表示修建的十字路的面積.
(2)若a=30,b=20,求草坪(陰影部分)的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
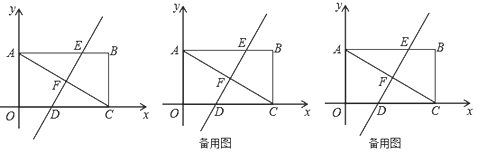
【題目】如圖,平面直角坐標系中,矩形![]() 的對角線
的對角線![]() ,
,![]() .
.
(1)把矩形![]() 沿直線
沿直線![]() 對折,使點
對折,使點![]() 落在點
落在點![]() 處,折痕
處,折痕![]() 分別與
分別與![]() 、
、![]() 、
、![]() 相交于點
相交于點![]() 、
、![]() 、
、![]() ,求直線
,求直線![]() 的解析式;
的解析式;
(2)若點![]() 在直線
在直線![]() 上,平面內是否存在點
上,平面內是否存在點![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形?若存在,請直接寫出點
為頂點的四邊形是菱形?若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)整式![]() 表示
表示![]() 、
、![]() 兩數和的平方
兩數和的平方
整式![]() 表示
表示![]() 、
、![]() 兩數差的平方
兩數差的平方
仿照上例填空:整式![]() 表示:______.
表示:______.
整式![]() 表示:______.
表示:______.
(2)試計算![]() 、
、![]() 取不同數值時,
取不同數值時,![]() 及
及![]() 的值填入下表:
的值填入下表:
| 當 | 當 | 當 | 當 |
| ||||
|
(3)根據上表,我發現的規律______.
(4)用發現的規律計算:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某購物網店在雙十一期間實行打折促銷活動,規定如下表:
次性購物不大于100元不打折,不大于300元但大于100元打九折,超過300元的部分打八折.
(1)王老師一次性購物600元,他實際付款多少元?
(2)若顧客在該網店一次性購物![]() 元,當
元,當![]() 低于300元但大于100元時,他實際付款多少元?當
低于300元但大于100元時,他實際付款多少元?當![]() 大于300元時,他實際付款多少元?(用含
大于300元時,他實際付款多少元?(用含![]() 的式子表示)
的式子表示)
(3)如果王老師兩次購物貨款合計820元,第一次購物的貨款為![]() 元
元![]() ,用含
,用含![]() 的式子表示兩次購物王老師實際付款多少元?
的式子表示兩次購物王老師實際付款多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O是直線AB上一點,OC為任意一條射線,OD平分∠BOC,OE平分∠AOC.
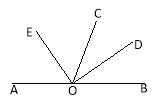
(1)指出圖中∠AOD與∠BOE的補角;
(2)試判斷∠COD與∠COE具有怎樣的數量關系.并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com