
【題目】如圖,在![]() 中,
中, ![]() ,
,![]() ,
, ![]() 是由
是由![]() 繞點
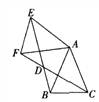
繞點![]() 按順時針方向旋轉得到的,連接
按順時針方向旋轉得到的,連接![]() 、
、![]() 相交于點
相交于點![]() .
.
(1)求證: ![]() ;
;
(2)當四邊形![]() 為菱形時,求
為菱形時,求![]() 的長.
的長.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(1)先由旋轉的性質得AE=AB,AF=AC,∠EAF=∠BAC,則∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根據旋轉的定義,△AEB可由△AFC繞點A按順時針方向旋轉得到,然后根據旋轉的性質得到BE=CD;
(2)由菱形的性質得到DE=AE=AC=AB=1,AC∥DE,根據等腰三角形的性質得∠AEB=∠ABE,根據平行線得性質得∠ABE=∠BAC=45°,所以∠AEB=∠ABE=45°,于是可判斷△ABE為等腰直角三角形,所以BE=![]() AC=
AC=![]() ,于是利用BD=BE-DE求解.
,于是利用BD=BE-DE求解.
試題解析:(1)證明:∵△AEF是由△ABC繞點A按順時針方向旋轉得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC繞點A按順時針方向旋轉得到,
∴BE=CF;
(2)解:∵四邊形ACDE為菱形,AB=AC=1,
∴DE=AE=AC=AB=1,AC∥DE,
∴∠AEB=∠ABE,∠ABE=∠BAC=45°,
∴∠AEB=∠ABE=45°,
∴△ABE為等腰直角三角形,
∴BE=![]() AC=
AC=![]() ,
,
∴BD=BE-DE=![]() -1.
-1.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】小剛在課外書中看到這樣一道有理數的混合運算題:
計算:![]()
她發現,這個算式反映的是前后兩部分的和,而這兩部分之間存在著某種關系,利用這種關系,他順利地解答了這道題。
(1)前后兩部分之間存在著什么關系?
(2)先計算哪步分比較簡便?并請計算比較簡便的那部分。
(3)利用(1)中的關系,直接寫出另一部分的結果。
(4)根據以上分析,求出原式的結果。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,在ABCD中,E、F為對角線AC上的兩點,且AE=CF,連接DE、BF,
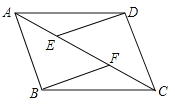
(1)寫出圖中所有的全等三角形;
(2)求證:DE∥BF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,請在下列四個關系中,選出兩個恰當的關系作為條件,推出四邊形ABCD是平行四邊形,并予以證明.(寫出一種即可)
關系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四邊形ABCD中, , ;
求證:四邊形ABCD是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
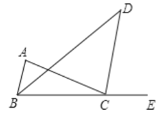
【題目】如圖,AC、BD相交于點O,∠A=∠ABC,∠DBC=∠D,BD平分∠ABC,點E在BC的延長線上。
(1)求證:CD∥AB;
(2)若∠D=38°,求∠ACE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形紙片ABCD(AD>AB)中,將它折疊,使點A與C重合,折痕EF交AD于E,交BC于F,交AC于O,連結AF、CE. 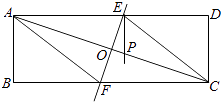
(1)求證:四邊形AFCE是菱形;
(2)過E作EP⊥AD交AC于P,求證:AE2=AOAP;
(3)若AE=8,△ABF的面積為9,求AB+BF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2013年1月,由于霧霾天氣持續籠罩我國中東部大部分地區,口罩市場出現熱賣,某旗艦網店用8000元購進甲、乙兩種口罩,銷售完后共獲利2800元,進價和售價如下表:
品名 | 甲種口罩 | 乙種口罩 |
進價(元/袋) | 20 | 25 |
售價(元/袋) | 26 | 35 |
(1)求該網店購進甲、乙兩種口罩各多少袋?
(2)該網店第二次以原價購進甲、乙、兩種口罩,購進乙種口罩袋數不變,而購進甲種口罩袋數是第一次的2倍.甲種口罩按原售價出售,而乙種口罩讓利銷售.若兩種口罩銷售完畢,要使第二次銷售活動獲利不少于3680元,乙種口罩最低售價為每袋多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在菱形ABCD中,對角線AC、BD相交于點O,DE∥AC,AE∥BD.

(1)求證:四邊形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四邊形AODE的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com