
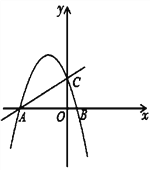
【題目】已知在平面直角坐標系中,拋物線![]() 與x軸相交于點A,B,與y軸相交于點C. 已知A,C兩點的坐標分別為A(-4,0), C(0,4).
與x軸相交于點A,B,與y軸相交于點C. 已知A,C兩點的坐標分別為A(-4,0), C(0,4).
(1)求拋物線的表達式;
(2)如果點P,Q在拋物線上(P點在對稱軸左邊),且PQ∥AO,PQ=2AO,求P,Q的坐標;
(3)動點M在直線y=x+4上,且△ABC與△COM相似,求點M的坐標.
【答案】(1)![]() ;
;
(2)P點坐標(-5,![]() ),Q點坐標(3,
),Q點坐標(3,![]() );
);
(3)M點的坐標為(![]() ,
,![]() ),(-3,1).
),(-3,1).
【解析】分析:(1)根據待定系數法,可得函數解析式;
(2)根據平行于x軸的直線與拋物線的交點關于對稱軸對稱,可得P、Q關于直線x=-1對稱,根據PQ的長,可得P點的橫坐標,Q點的橫坐標,根據自變量與函數值的對應關系,可得答案;
(3)根據兩組對邊對應成比例且夾角相等的兩個三角形相似,可得CM的長,根據等腰直角三角形的性質,可得MH的長,再根據自變量與函數值的對應關系,可得答案.
解:(1)將A、C點坐標代入函數解析式,
得 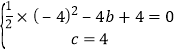 ,
,
解得![]() ,
,
∴拋物線的表達式為![]() ;
;
(2)PQ=2AO=8,
又PQ∥AO,即P、Q關于對稱軸x=﹣1對稱,
PQ=8,﹣1﹣4=﹣5,
當x=﹣5時,y=![]() ×(-5)2-(-5)+4=
×(-5)2-(-5)+4=![]() ,即P(-5,
,即P(-5,![]() );
);
﹣1+4=3,即Q(3,![]() );
);
P點坐標(-5,![]() ),Q點坐標(3,
),Q點坐標(3,![]() );
);
(3)∠MCO=∠CAB=45°,
①當△MCO∽△CAB時,
![]() ,
,
即![]() ,
,
CM=![]() .
.
如圖1,
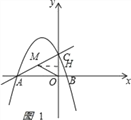
過M作MH⊥y軸于H,
MH=CH=![]() CM=
CM=![]() ,
,
當x=![]() 時,y=
時,y=![]() +4=
+4=![]() ,
,
∴M(![]() ,
,![]() );
);
②當△OCM∽△CAB時,
![]() ,
,
即![]() ,
,
解得CM=![]() ,
,
如圖2,
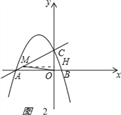
過M作MH⊥y軸于H,MH=CH=![]() CM=3,
CM=3,
當x=﹣3時,y=﹣3+4=1,
∴M(﹣3,1)
綜上所述:M點的坐標為(![]() ,
,![]() ),(-3,1).
),(-3,1).


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:初中數學 來源: 題型:
【題目】廣州火車南站廣場計劃在廣場內種植A,B兩種花木共 6600棵,若A花木數量是B花木數量的2倍少600棵.
(1)A,B兩種花木的數量分別是多少棵?
(2)如果園林處安排26人同時種植這兩種花木,每人每天能種植A花木60棵或B花木40棵,應分別安排多少人種植A花木和B花木,才能確保同時完成各自的任務?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() =
=![]() (
(![]() ≠0)與
≠0)與![]() 軸交于AB兩點,與
軸交于AB兩點,與![]() 軸交于C點,其對稱軸為
軸交于C點,其對稱軸為![]() =1,且A(-1,0)C(0,2).
=1,且A(-1,0)C(0,2).
(1)直接寫出該拋物線的解析式;
(2)P是對稱軸上一點,△PAC的周長存在最大值還是最小值?請求出取得最值(最大值或最小值)時點P的坐標;
(3)設對稱軸與![]() 軸交于點H,點D為線段CH上的一動點(不與點CH重合).點P是(2)中所求的點.過點D作DE∥PC交
軸交于點H,點D為線段CH上的一動點(不與點CH重合).點P是(2)中所求的點.過點D作DE∥PC交![]() 軸于點E.連接PDPE.若CD的長為
軸于點E.連接PDPE.若CD的長為![]() ,△PDE的面積為S,求S與
,△PDE的面積為S,求S與![]() 之間的函數關系式,試說明S是否存在最值,若存在,請求出最值,并寫出S取得的最值及此時
之間的函數關系式,試說明S是否存在最值,若存在,請求出最值,并寫出S取得的最值及此時![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
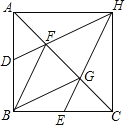
【題目】已知:如圖,在△ABC中,AB=BC,∠ABC=90°,點D、E分別是邊AB、BC的中點,點F、G是邊AC的三等分點,DF、EG的延長線相交于點H,連接HA、HC.
(1)求證:四邊形FBGH是菱形;
(2)求證:四邊形ABCH是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD的軌道上有兩個點甲與乙,開始時甲在A處,乙在C處,它們沿著正方形軌道順時針同時出發,甲的速度為每秒1 cm,乙的速度為每秒5 cm,已知正方形軌道ABCD的邊長為2 cm,則乙在第2 020次追上甲時的位置在( )
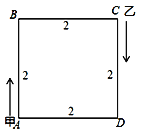
A.AB上B.BC上
C.CD上D.AD上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校要從甲乙兩名射擊運動員中挑選一人參加全市比賽,在選拔賽中,每人進行了5次射擊,甲的成績(環)為:9.7,10,9.6,9.8,9.9;乙的成績的平均數為9.8,方差為0.032;
(1)甲的射擊成績的平均數和方差分別是多少?
(2)據估計,如果成績的平均數達到9.8環就可能奪得金牌,為了奪得金牌,應選誰參加比賽?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點![]() ,
,![]() 在數軸上分別表示有理數
在數軸上分別表示有理數![]() ,
,![]() ,
,![]() ,
,![]() 兩點之間的距離表示為
兩點之間的距離表示為![]() ,在數軸上
,在數軸上![]() ,
,![]() 兩點之間的距離
兩點之間的距離![]() .已知數軸上
.已知數軸上![]() ,
,![]() 兩點表示數
兩點表示數![]() ,
,![]() 滿足
滿足![]() ,點
,點![]() 為數軸上一動點,其對應的數為
為數軸上一動點,其對應的數為![]() .
.
![]()
(1)![]() ,
,![]() 兩點之間的距離是.
兩點之間的距離是.
(2)![]() 與
與![]() 之間的距離表示為.
之間的距離表示為.
(3)數軸上是否存在點![]() ,使點
,使點![]() 到點
到點![]() ,點
,點![]() 的距離之和為
的距離之和為![]() ?若存在,請求出
?若存在,請求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
(4)現在點![]() ,點
,點![]() 分別以
分別以![]() 單位/秒和
單位/秒和![]() 單位/秒的速度同時向右運動,當點
單位/秒的速度同時向右運動,當點![]() 與點
與點![]() 之間的距離為
之間的距離為![]() 個單位長度時,求點
個單位長度時,求點![]() 所對應的數是多少?
所對應的數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD中,∠B=60°,點E在邊BC上,點F在邊CD上.
(1)如圖①,若點E是BC的中點,∠AEF=60°,求證:BE=DF;
(2)如圖②,若∠EAF=60°,求證:△AEF是等邊三角形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com