
【題目】《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架,書中的算法體系至今仍在推動著計算機的發展和應用.《九章算術》中記載:今有戶不知高、廣,竿不知長、短.橫之不出四尺,從之不出二尺,邪之適出.問戶高、廣、邪各幾何?譯文是:今有門不知其高、寬,有竿,不知其長、短,橫放,竿比門寬長出![]() 尺;豎放,竿比門高長出
尺;豎放,竿比門高長出![]() 尺;斜放,竿與門對角線恰好相等.問門高、寬、對角線長分別是多少?若設門對角線長為
尺;斜放,竿與門對角線恰好相等.問門高、寬、對角線長分別是多少?若設門對角線長為![]() 尺,則可列方程為__________.
尺,則可列方程為__________.
科目:初中數學 來源: 題型:
【題目】元旦前夕,湖州吳興某工藝廠設計了一款成本10元/件的工藝品投放市場試銷.試銷發現,每天銷售量y(件)與銷售單價x(元/件)之間的關系可近似地看作一次函數:y=-10x+700. (利潤=銷售總價-成本總價)
⑴ 如果該廠想要每天獲得5000元的利潤,那么銷售單價應定為多少元/件?
⑵ 當銷售單價定為多少時,工藝廠試銷該工藝品每天獲得的利潤最大?最大利潤是多少?
⑶ 湖州市物價部門規定,該工藝品銷售單價最高不能超過38元/件,那么銷售單價定為多少時,工藝廠試銷該工藝品每天獲得的利潤最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2011年國家對“酒后駕車”加大了處罰力度,出臺了不準酒后駕車的禁令.某記者在一停車場對開車的司機進行了相關的調查,本次調查結果有四種情況:①偶爾喝點酒后開車;②已戒酒或從來不喝酒;③喝酒后不開車或請專業司機代駕;④平時喝酒,但開車當天不喝酒.將這次調查悄況整理并繪制了如下尚不完整的統計圖,請根據相關信息,解答下列問題
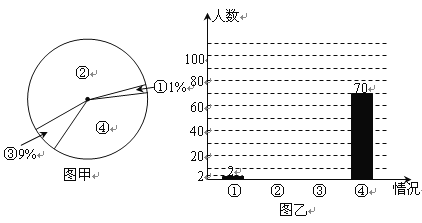
(1)該記者本次一共調查了 名司機.
(2)求圖甲中④所在扇形的圓心角,并補全圖乙.
(3)在本次調查中,記者隨機采訪其中的一名司機,求他屬第②種情況的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某風景區集體門票的收費標準是30人以內(含30人),每人25元;超過30人,超過部分每人10元.
(1)寫出應收門票費![]() (元)與游覽人數
(元)與游覽人數![]() (人)之間的函數關系式;
(人)之間的函數關系式;
(2)利用(1)中的函數關系式計算,某班54人去該風景區旅游時,為購門票共花了多少元.
查看答案和解析>>
科目:初中數學 來源: 題型:
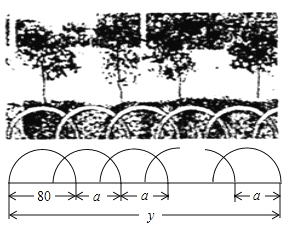
【題目】如圖所示,某花園護欄是用直徑為![]() 的半圓形條鋼組制而成,且每增加一個半圓形條鋼,護欄長度增加
的半圓形條鋼組制而成,且每增加一個半圓形條鋼,護欄長度增加![]() ,設半圓形條鋼的個數為
,設半圓形條鋼的個數為![]() (
(![]() 為正整數),護欄總長度為
為正整數),護欄總長度為![]() .
.
(1)若![]() .
.
①當![]() 時,y=______
時,y=______![]() ;
;
②寫出![]() 與
與![]() 之間的函數關系式為_______.
之間的函數關系式為_______.
(2)若護欄總長度為![]() ,則當
,則當![]() 時,所用半圓形條鋼個數為_______;
時,所用半圓形條鋼個數為_______;
(3)若護欄總長度不變,則當![]() 時,用了
時,用了![]() 個半圓形條鋼;當
個半圓形條鋼;當![]() 時,用了
時,用了![]() 個半圓形條鋼.請求出
個半圓形條鋼.請求出![]() 與
與![]() 之間的關系式.
之間的關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
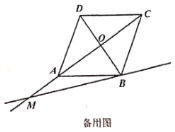
【題目】如圖,![]() 為菱形
為菱形![]() 對角線的交點,
對角線的交點,![]() 是射線
是射線![]() 上的一個動點(點
上的一個動點(點![]() 與點
與點![]() ,
,![]() ,
,![]() 都不重合),過點
都不重合),過點![]() ,
,![]() 分別向直線
分別向直線![]() 作垂線段,垂足分別為
作垂線段,垂足分別為![]() ,
,![]() ,連接
,連接![]() ,
,![]() .
.
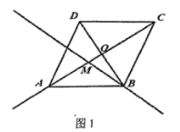
(1)①當點![]() 在線段
在線段![]() 上時,在圖1中依據題意補全圖形:
上時,在圖1中依據題意補全圖形:
②猜想![]() 與
與![]() 的數量關系為 .
的數量關系為 .
(2)小東通過觀察、實驗發現點![]() 在線段
在線段![]() 的延長線上運動時,(1)中的猜想始終成立.
的延長線上運動時,(1)中的猜想始終成立.
小東把這個發現與同學們進行交流,通過討論,形成了證明此猜想的幾種想法:
想法1:由已知條件和菱形對角線互相平分,可以構造與![]() 全等的三角形,從而得到相等的錢段,再依據直角三角形斜邊中線的性質,即可證明猜想;
全等的三角形,從而得到相等的錢段,再依據直角三角形斜邊中線的性質,即可證明猜想;
想法2:由已知條件和菱形對角線互相垂直,能找到兩組共斜邊的直角三角形,例如其中的一組![]() 和
和![]() ,再依據直角三角形斜邊中線的性質,菱形四條邊相等,可以構造一對以
,再依據直角三角形斜邊中線的性質,菱形四條邊相等,可以構造一對以![]() 和
和![]() 為對應邊的全等三角形,即可證明猜想.
為對應邊的全等三角形,即可證明猜想.
…
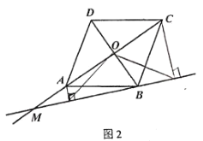
請你參考上面的想法,在圖2中幫助小東完成畫圖,并證明此猜想(一種方法即可).
(3)當![]() 時,請直接寫出線段
時,請直接寫出線段![]() ,
,![]() ,
,![]() 之間的數量關系是 .
之間的數量關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“一帶一路”戰略為民營快遞企業轉變為跨境物流商提供了機遇.也讓國民可以足不出戶地買到世界各國的商品.小絲購買了一些物品,并了解到兩家快遞公司的收費方式.
甲公司:物品重量不超過1千克的,需付費20元,超過1千克的部分按每千克4元計價.
乙公司:按物品重量每千克7元計價,外加一份包裝費10元.
設物品的重量為![]() 千克,甲、乙公司快遞該物品的費用分別為
千克,甲、乙公司快遞該物品的費用分別為![]() .
.
(1)寫出![]() 與
與![]() 的函數表達式,并寫出自變量
的函數表達式,并寫出自變量![]() 的取值范圍;
的取值范圍;
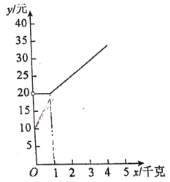
(2)圖中給出了![]() 與
與![]() 的函數圖象,請在圖中畫出(1)中的函數圖象;
的函數圖象,請在圖中畫出(1)中的函數圖象;
(3)小絲需要快遞的物品重量為4千克,如果想節省快遞費用,結合圖象指出,應選擇的快遞公司是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,O為AC中點,過點O的直線分別與AB,CD交于點E,F,連結BF,交AC于點M,連結DE,BO.若∠BOC=60°,FO=FC,則下列結論:①AE=CF;②BF垂直平分線段OC;③△EOB≌△CMB;④四邊形是BFDE菱形.其中正確結論的個數是( )

A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=13 cm,AC=20 cm,BC邊上的高為12 cm,則△ABC的面積是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com