【題目】在平面坐標系中，正方形ABCD的位置如圖所示，點A的坐標為（1，0），點D的坐標為（0，2），延長CB交x軸于點A1 ， 作正方形A1B1C1C，延長C1B1交x軸于點A2 ， 作正方形A2B2C2C1,………按這樣的規律進行下去，第2012個正方形的面積為（ ）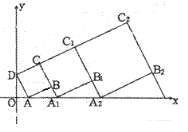
A.
B.
C.
D.
【答案】D
【解析】因為點A的坐標為(1，0)，點D的坐標為(0，2)，
∴OA=1，OD=2，
設正方形的面積分別為 
, 
… 
，
根據題意,得：AD∥BC∥ 
∥ 
，
∴ 
= 
= 
，
∵ 
，
∴ 
∽ 
，
在直角△ADO中,根據勾股定理,，得：AD= 
，
∴AB=AD=BC= 
，
∴ =5，
∵∠DAO+∠ADO=90°,∠DAO+ =90°，
∴∠ADO= ，
∴tan = 
，
∴ 
，
∴ 
=BC+ 
= 
，
∴ = 
×5=5× 
，
∴ 
，
∴ 
,
∴ 
，
∴ 
S3=8116×5=5×(32)4，
由此可得： 
，
∴ 
.
故答案為：D.
根據勾股定理求出第一個正方形的邊長，求出第一個正方形的面積；由三角函數值求出第二個正方形的面積···；由規律得到第2012個正方形的面積.
品學雙優卷系列答案
小學期末沖刺100分系列答案
期末復習檢測系列答案科目：初中數學 來源： 題型：
【題目】如圖，平行于x軸的直線AC分別交拋物線 
（x≥0）與 
（x≥0）于B、C兩點，過點C作y軸的平行線交y1于點D，直線DE∥AC，交y2于點E，則 
= ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列條件中，不能判斷四邊形ABCD是平行四邊形的為( )
A. AB∥CD，AD∥BC
B. AB＝CD，AD＝BC
C. AB∥CD，AD＝BC
D. AB∥CD，AB＝CD
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在正方形ABCD中，AC是對角線，今有較大的直角三角板，一邊始終經過點B，直角頂點P在射線AC上移動，另一邊交DC于點Q.
(1)如圖①，當點Q在DC邊上時，猜想并寫出PB與PQ所滿足的數量關系，并加以證明；
(2)如圖②，當點Q落在DC的延長線上時，猜想并寫出PB與PQ滿足的數量關系，并證明你的猜想．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠ABE=∠ACD=Rt∠，AE=AD，∠ABC=∠ACB.求證：∠BAE=∠CAD．
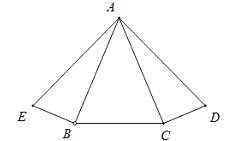
請補全證明過程，并在括號里寫上理由．
證明：在△ABC中，
∵∠ABC=∠ACB
∴AB= （ ）
在Rt△ABE和Rt△ACD中，
∵ =AC， =AD
∴Rt△ABE≌Rt△ACD（ ）
∴∠BAE=∠CAD（ ）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形ABCD中，AD＝6，DC＝8，菱形EFGH的三個頂點E、G、H分別在矩形ABCD的邊AB、CD、DA上，AH＝2.
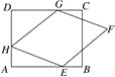
(1)已知DG＝6，求AE的長；
(2)已知DG＝2，求證：四邊形EFGH為正方形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，∠ABC=30°，AB=6，點D是BC上一動點，連接AD，將△ACD沿AD折疊，點C落在點C1處，連接C1B，則BC1的最小值為（ ） 
A.2
B.3
C.3 
D.2 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】完成下面的證明
如圖，FG//CD，∠1=∠3，∠B=50°，求∠BDE的度數.
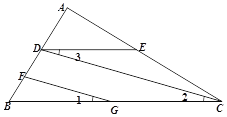
解：∵FG//CD (已知)
∴∠2=_________（____________________________）
又∵∠1=∠3，
∴∠3=∠2（等量代換）
∴BC//__________（_____________________________）
∴∠B+________=180°（______________________________）
又∵∠B=50°
∴∠BDE=________________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】A、B兩市相距150千米，分別從A、B處測得國家級風景區中心C處的方向角如圖所示，風景區區域是以C為圓心，45千米為半徑的圓，tanα=1.627，tanβ=1.373．為了開發旅游，有關部門設計修建連接AB兩市的高速公路．問連接AB高速公路是否穿過風景區，請說明理由．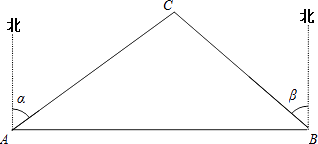
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com