
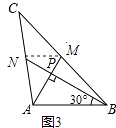
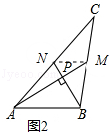
【題目】愛好思考的小茜在探究兩條直線的位置關系查閱資料時,發現了“中垂三角形”,即兩條中線互相垂直的三角形稱為“中垂三角形”.如圖(1)、圖(2)、圖(3)中,AM、BN是△ABC的中線,AM⊥BN于點P,像△ABC這樣的三角形均為“中垂三角形”.設BC=a,AC=b,AB=c.
(1)如圖1,當tan∠PAB=1,c=4 ![]() 時,a= , b=;
時,a= , b=;
如圖2,當∠PAB=30°,c=2時,a= , b=;
(2)請你觀察(1)中的計算結果,猜想a2、b2、c2三者之間的關系,用等式表示出來,并利用圖3證明你的結論.
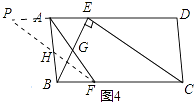
(3)如圖4,ABCD中,E、F分別是AD、BC的三等分點,且AD=3AE,BC=3BF,連接AF、BE、CE,且BE⊥CE于E,AF與BE相交點G,AD=3 ![]() ,AB=3,求AF的長.
,AB=3,求AF的長.
【答案】
(1)4 ![]() ;4
;4 ![]() ;
;![]() ;
;![]()
(2)
解:結論a2+b2=5c2.
證明:如圖3中,連接MN.
∵AM、BN是中線,
∴MN∥AB,MN= ![]() AB,
AB,
∴△MPN∽△APB,
∴ ![]() =
= ![]() =
= ![]() ,
,
設MP=x,NP=y,則AP=2x,BP=2y,
∴a2=BC2=4BM2=4(MP2+BP2)=4x2+16y2,
b2=AC2=4AN2=4(PN2+AP2)=4y2+16x2,
c2=AB2=AP2+BP2=4x2+4y2,
∴a2+b2=20x2+20y2=5(4x2+4y2)=5c2
(3)
解:如圖4中,在△AGE和△FGB中,
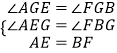 ,
,
∴△AGE≌△FGB,
∴BG=FG,取AB中點H,連接FH并且延長交DA的延長線于P點,
同理可證△APH≌△BFH,
∴AP=BF,PE=CF=2BF,
即PE∥CF,PE=CF,
∴四邊形CEPF是平行四邊形,
∴FP∥CE,
∵BE⊥CE,
∴FP⊥BE,即FH⊥BG,
∴△ABF是中垂三角形,
由(2)可知AB2+AF2=5BF2,
∵AB=3,BF= ![]() AD=
AD= ![]() ,
,
∴9+AF2=5×( ![]() )2,
)2,
∴AF=4.
【解析】(1)解:如圖1中,∵CN=AN,CM=BM,
∴MN∥AB,MN= ![]() AB=2
AB=2 ![]() ,
,
∵tan∠PAB=1,
∴∠PAB=∠PBA=∠PNM=∠PMN=45°,
∴PN=PM=2,PB=PA=4,
∴AN=BM= ![]() =2
=2 ![]() .
.
∴b=AC=2AN=4 ![]() ,a=BC=4
,a=BC=4 ![]() .
.
故答案為4 ![]() ,4
,4 ![]() ,
,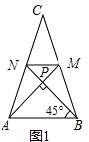
如圖2中,連接NM,
, ∵CN=AN,CM=BM,
∴MN∥AB,MN= ![]() AB=1,
AB=1,
∵∠PAB=30°,
∴PB=1,PA= ![]() ,
,
在RT△MNP中,∵∠NMP=∠PAB=30°,
∴PN= ![]() ,PM=
,PM= ![]() ,
,
∴AN= ![]() ,BM=
,BM= ![]() ,
,
∴a=BC=2BM= ![]() ,b=AC=2AN=
,b=AC=2AN= ![]() ,
,
故答案分別為 ![]() ,
, ![]() .
.
(1)①首先證明△APB,△PEF都是等腰直角三角形,求出PA、PB、PN、PM,再利用勾股定理即可解決問題.②連接MN,在RT△PAB,RT△PMN中,利用30°性質求出PA、PB、PN、PM,再利用勾股定理即可解決問題.(2)結論a2+b2=5c2 . 設MP=x,NP=y,則AP=2x,BP=2y,利用勾股定理分別求出a2、b2、c2即可解決問題.(3)取AB中點H,連接FH并且延長交DA的延長線于P點,首先證明△ABF是中垂三角形,利用(2)中結論列出方程即可解決問題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
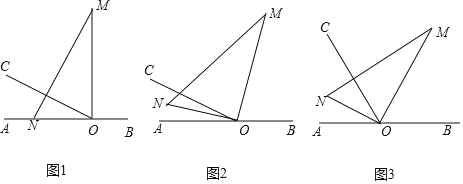
【題目】如圖1,O為直線AB上一點,過點O作射線OC,∠AOC=30°,將一直角三角板(∠M=30°)的直角頂點放在點O處,一邊ON在射線OA上,另一邊OM與OC都在直線AB的上方.
(1)將圖1中的三角板繞點O以每秒3°的速度沿順時針方向旋轉一周.如圖2,經過t秒后OM恰好平分∠BOC,則t= (直接寫結果)
(2)在(1)問的基礎上,若三角板在轉動的同時,射線OC也繞O點以每秒6°的速度沿順時針方向旋轉一周,如圖3,那么經過多少秒后OC平分∠MON?請說明理由;
(3)在(2)問的基礎上,那么經過多少秒∠MOC=36°?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】菱形ABCD中,∠B=60°,點E在邊BC上,點F在邊CD上.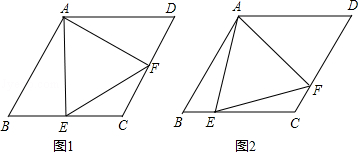
(1)如圖1,若E是BC的中點,∠AEF=60°,求證:BE=DF;
(2)如圖2,若∠EAF=60°,求證:△AEF是等邊三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,在河的兩岸有A,B兩個村莊,河寬為4千米,A、B兩村莊的直線距離 AB=10千米,A、B兩村莊到河岸的距離分別為1千米、3千米,計劃在河上修建一座橋MN垂直于兩岸,M點為靠近A村莊的河岸上一點,求AM+BN的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,把△ABC繞A點沿順時針方向旋轉得到△ADE,連接BD,CE交于點F. 
(1)求證:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,當四邊形ADFC是菱形時,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 經過第一象限的點
經過第一象限的點![]() 和點
和點![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,
,![]() 的面積為
的面積為![]() .
.
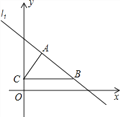
![]() 求
求![]() 點的坐標;
點的坐標;
![]() 求直線
求直線![]() 的函數表達式;
的函數表達式;
![]() 直線
直線![]() 經過線段
經過線段![]() 上一點
上一點![]() (
(![]() 不與
不與![]() 、
、![]() 重合),求
重合),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知甲、乙兩人均從400米的環形跑道的A處出發,各自以每秒6米和每秒8米的速度在跑道上跑步.
(1)若兩人同時出發,背向而行,則經過 秒鐘兩人第一次相遇;若兩人同時出發,同向而行,則經過 秒鐘乙第一次追上甲.
(2)若兩人同向而行,乙在甲出發10秒鐘后去追甲,經過多少時間乙第二次追上甲.
(3)若讓甲先跑10秒鐘后乙開始跑,在乙用時不超過100秒的情況下,乙跑多少秒鐘時,兩人相距40米.
查看答案和解析>>
科目:初中數學 來源: 題型:
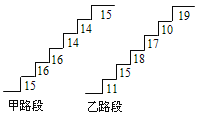
【題目】在某旅游景區上山的一條小路上,有一些斷斷續續的臺階,下圖是其中的甲、乙兩段臺階的示意圖,圖中的數字表示每一級臺階的高度(單位:cm).請你用所學過的有關統計知識,回答下列問題(數據:15,16,16,14,14,15的方差![]() ,數據:11,15,18,17,10,19的方差
,數據:11,15,18,17,10,19的方差![]() :
:
(1)分別求甲、乙兩段臺階的高度平均數;
(2)哪段臺階走起來更舒服?與哪個數據(平均數、中位數、方差和極差)有關?
(3)為方便游客行走,需要陳欣整修上山的小路,對于這兩段臺階路.在總高度及臺階數不變的情況下,請你提出合理的整修建議.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com