
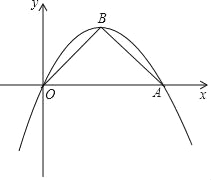
【題目】如圖,在平面直角坐標(biāo)系xOy,已知二次函數(shù)y=﹣![]() x2+bx的圖象過點(diǎn)A(4,0),頂點(diǎn)為B,連接AB、BO.
x2+bx的圖象過點(diǎn)A(4,0),頂點(diǎn)為B,連接AB、BO.
(1)求二次函數(shù)的表達(dá)式;
(2)若C是BO的中點(diǎn),點(diǎn)Q在線段AB上,設(shè)點(diǎn)B關(guān)于直線CQ的對(duì)稱點(diǎn)為B',當(dāng)△OCB'為等邊三角形時(shí),求BQ的長度;
(3)若點(diǎn)D在線段BO上,OD=2DB,點(diǎn)E、F在△OAB的邊上,且滿足△DOF與△DEF全等,求點(diǎn)E的坐標(biāo).
【答案】(1)二次函數(shù)的表達(dá)式為y=﹣![]() x2+2x;(2)BQ=
x2+2x;(2)BQ=![]() ;(3)點(diǎn)E的坐標(biāo)為:(
;(3)點(diǎn)E的坐標(biāo)為:(![]() ,0)或(
,0)或(![]() ,
,![]() )或(2+
)或(2+![]() ,2﹣
,2﹣![]() )或(4,0).
)或(4,0).
【解析】試題分析:(1)利用待定系數(shù)法求二次函數(shù)的表達(dá)式;
(2)先求出OB和AB的長,根據(jù)勾股定理的逆定理證明∠ABO=90°,由對(duì)稱計(jì)算∠QCB=60°,利用特殊的三角函數(shù)列式可得BQ的長;
(3)因?yàn)镈在OB上,所以F分兩種情況:
i)當(dāng)F在邊OA上時(shí),ii)當(dāng)點(diǎn)F在AB上時(shí),
當(dāng)F在邊OA上時(shí),分三種情況:
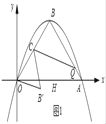
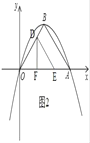
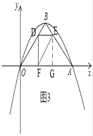
①如圖2,過D作DF⊥x軸,垂足為F,則E、F在OA上,②如圖3,作輔助線,構(gòu)建△OFD≌△EDF≌△FGE,③如圖4,將△DOF沿邊DF翻折,使得O恰好落在AB邊上,記為點(diǎn)E;當(dāng)點(diǎn)F在OB上時(shí),過D作DF∥x軸,交AB于F,連接OF與DA,依次求出點(diǎn)E的坐標(biāo)即可.
試題解析:(1)將點(diǎn)A的坐標(biāo)代入二次函數(shù)的解析式得:﹣![]() ×42+4b=0,解得b=2,
×42+4b=0,解得b=2,
∴二次函數(shù)的表達(dá)式為y=﹣![]() x2+2x.
x2+2x.
(2)∵y=﹣![]() x2+2x=﹣
x2+2x=﹣![]() (x﹣2)2+2,
(x﹣2)2+2,
∴B(2,2),拋物線的對(duì)稱軸為x=2.
如圖1所示:
由兩點(diǎn)間的距離公式得:OB=![]() =2
=2![]() ,BA=
,BA=![]() =2
=2![]() .
.
∵C是OB的中點(diǎn),
∴OC=BC=![]() .
.
∵△OB′C為等邊三角形,
∴∠OCB′=60°.
又∵點(diǎn)B與點(diǎn)B′關(guān)于CQ對(duì)稱,
∴∠B′CQ=∠BCQ=60°.
∵OA=4,OB=2![]() ,AB=2
,AB=2![]() ,
,
∴OB2+AB2=OA2,
∴∠OBA=90°.
在Rt△CBQ中,∠CBQ=90°,∠BCQ=60°,BC=![]() ,
,
∴tan60°=![]() ,
,
∴BQ=![]() CB=
CB=![]() ×
×![]() =
=![]() .
.
(3)分兩種情況:
i)當(dāng)F在邊OA上時(shí),
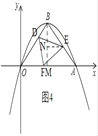
①如圖2,過D作DF⊥x軸,垂足為F,
∵△DOF≌△DEF,且E在線段OA上,
∴OF=FE,
由(2)得:OB=2![]() ,
,
∵點(diǎn)D在線段BO上,OD=2DB,
∴OD=![]() OB=
OB=![]() ,
,
∵∠BOA=45°,
∴cos45°=![]() ,
,
∴OF=ODcos45°=![]() =
=![]() ,
,
則OE=2OF=![]() ,
,
∴點(diǎn)E的坐標(biāo)為(![]() ,0);
,0);
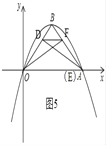
②如圖3,過D作DF⊥x軸于F,過D作DE∥x軸,交AB于E,連接EF,過E作EG⊥x軸于G,
∴△BDE∽△BOA,
∴![]() =
=![]() ,
,
∵OA=4,
∴DE=![]() ,
,
∵DE∥OA,
∴∠OFD=∠FDE=90°,
∵DE=OF=![]() ,DF=DF,
,DF=DF,
∴△OFD≌△EDF,
同理可得:△EDF≌△FGE,
∴△OFD≌△EDF≌△FGE,
∴OG=OF+FG=OF+DE=![]() +
+![]() =
=![]() ,EG=DF=ODsin45°=
,EG=DF=ODsin45°=![]() ,
,
∴E的坐標(biāo)為(![]() ,
,![]() );
);
③如圖4,將△DOF沿邊DF翻折,使得O恰好落在AB邊上,記為點(diǎn)E,
過B作BM⊥x軸于M,過E作EN⊥BM于N,
由翻折的性質(zhì)得:△DOF≌△DEF,
∴OD=DE=![]() ,
,
∵BD=![]() OD=
OD=![]() ,
,
∴在Rt△DBE中,由勾股定理得:BE=![]() =
=![]() ,
,
則BN=NE=BEcos45°=![]() ×
×![]() =
=![]() ,
,
OM+NE=2+![]() ,BM﹣BN=2﹣
,BM﹣BN=2﹣![]() ,
,
∴點(diǎn)E的坐標(biāo)為:(2+![]() ,2﹣
,2﹣![]() );
);
ii)當(dāng)點(diǎn)F在AB上時(shí),
過D作DF∥x軸,交AB于F,連接OF與DA,
∵DF∥x軸,
∴△BDF∽△BOA,
∴![]() ,
,
由拋物線的對(duì)稱性得:OB=BA,
∴BD=BF,
則∠BDF=∠BFD,∠ODF=∠AFD,
∴OD=OB﹣BD=BA﹣BF=AF,
則△DOF≌△DAF,
∴E和A重合,則點(diǎn)E的坐標(biāo)為(4,0);
綜上所述,點(diǎn)E的坐標(biāo)為:(![]() ,0)或(
,0)或(![]() ,
,![]() )或(2+
)或(2+![]() ,2﹣
,2﹣![]() )或(4,0).
)或(4,0).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】當(dāng)x=2時(shí),代數(shù)式x2(2x)3﹣x(x+8x4)的值是( )
A.4
B.-4
C.0
D.1
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,D是△ABC的邊AB上一點(diǎn),CN∥AB,DN交AC于點(diǎn)M,若MA=MC. 
(1)求證:CD=AN;
(2)若AC⊥DN,∠CAN=30°,MN=1,求四邊形ADCN的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com