
【題目】已知,在直角三角形ABC中,∠ACB=90°,D是AB上一點,且∠ACD=∠B.
(1)如圖1,求證:CD⊥AB;
(2)將△ADC沿CD所在直線翻折,A點落在BD邊所在直線上,記為A′點.
①如圖2,若∠B=34°,求∠A′CB的度數;
②若∠B=n°,請直接寫出∠A′CB的度數(用含n的代數式表示).

【答案】(1)詳見解析;(2)①∠A'CB=22°;②∠A'CB=90°﹣2n°.
【解析】
(1)根據直角三角形的性質即可得出答案;
(2)①由∠ACD=∠B,得∠ACD=34°,再結合(1),得∠BCD=56°,再由折疊的性質即可得到答案;
②解題過程同①.
(1)∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵∠ACD=∠B,
∴∠B+∠BCD=90°,
∴∠BDC=90°,
∴CD⊥AB;
(2)①當∠B=34°時,∵∠ACD=∠B,
∴∠ACD=34°,
由(1)知,∠BCD+∠B=90°,
∴∠BCD=56°,
由折疊知,∠A'CD=∠ACD=34°,
∴∠A'CB=∠BCD﹣∠A'CD=56°﹣34°=22°;
②當∠B=n°時,同①的方法得,∠A'CD=n°,∠BCD=90°﹣n°,
∴∠A'CB=∠BCD﹣∠A'CD=90°﹣n°﹣n°=90°﹣2n°.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
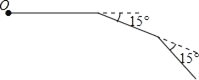
【題目】如圖,小明從點O出發,前進5m后向右轉15°,再前進5m后又向右轉15°,…這樣一直下去,直到他第一次回到出發點O為止,他所走的路徑構成了一個多邊形.
(1)小明一共走了多少米?
(2)這個多邊形的內角和是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
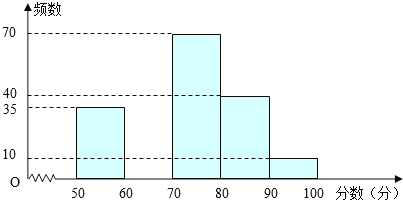
【題目】為創建“國家園林城市”,某校舉行了以“愛我黃石”為主題的圖片制作比賽,評委會對200名同學的參賽作品打分發現,參賽者的成績x均滿足50≤x<100,并制作了頻數分布直方圖,如圖.
根據以上信息,解答下列問題:
(1)請補全頻數分布直方圖;
(2)若依據成績,采取分層抽樣的方法,從參賽同學中抽40人參加圖片制作比賽總結大會,則從成績80≤x<90的選手中應抽多少人?
(3)比賽共設一、二、三等獎,若只有25%的參賽同學能拿到一等獎,則一等獎的分數線是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知BD垂直平分線段AC,∠BCD=∠ADF,AF⊥AC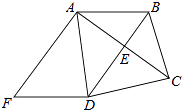
(1)證明:四邊形ABDF是平行四邊形;
(2)若AF=DF=5,AD=6,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知將一塊直角三角板DEF放置在△ABC上,使得該三角板的兩條直角邊DE,DF恰好分別經過點B、C.
(1)∠DBC+∠DCB= 度;
(2)過點A作直線直線MN∥DE,若∠ACD=20°,試求∠CAM的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖 AB=AC,CD⊥AB于D,BE⊥AC于E,BE與CD相交于點O.
(1)求證AD=AE;
(2)連接OA,BC,試判斷直線OA,BC的關系并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,A、B、C分別為數軸上的三點,A點對應的數為60,B點在A點的左側,并且與A點的距離為30,C點在B點左側,C點到A點距離是B點到A點距離的4倍.
![]()
(1)求出數軸上B點對應的數及AC的距離.
(2)點P從A點出發,以3單位/秒的速度向終點C運動,運動時間為t秒.
①當P點在AB之間運動時,則BP= .(用含t的代數式表示)
②P點自A點向C點運動過程中,何時P,A,B三點中其中一個點是另外兩個點的中點?求出相應的時間t.
③當P點運動到B點時,另一點Q以5單位/秒的速度從A點出發,也向C點運動,點Q到達C點后立即原速返回到A點,那么Q點在往返過程中與P點相遇幾次?直.接.寫.出.相遇時P點在數軸上對應的數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com