
【題目】如圖,菱形ABCD中,AB=2,∠A=120°,點P,Q,K分別為線段BC,CD,BD上的任意一點,則PK+QK的最小值為( ) 
A.1
B.![]()
C.2
D.![]() +1
+1
【答案】B
【解析】解:∵四邊形ABCD是菱形, ∴AD∥BC,
∵∠A=120°,
∴∠B=180°﹣∠A=180°﹣120°=60°,
作點P關于直線BD的對稱點P′,連接P′Q,P′C,則P′Q的長即為PK+QK的最小值,由圖可知,當點Q與點C重合,CP′⊥AB時PK+QK的值最小,
在Rt△BCP′中,
∵BC=AB=2,∠B=60°,
∴P′Q=CP′=BCsinB=2× ![]() =
= ![]() .
.
故選:B.
先根據四邊形ABCD是菱形可知,AD∥BC,由∠A=120°可知∠B=60°,作點P關于直線BD的對稱點P′,連接P′Q,PC,則P′Q的長即為PK+QK的最小值,由圖可知,當點Q與點C重合,CP′⊥AB時PK+QK的值最小,再在Rt△BCP′中利用銳角三角函數的定義求出P′C的長即可.


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數學 來源: 題型:
【題目】瑤寨中學食堂為學生提供了四種價格的午餐供其選擇,這四種價格分別是:A.3元,B.4元,C.5元,D.6元.為了了解學生對四種午餐的購買情況,學校隨機抽樣調查了甲、乙兩班學生某天購買四種午餐的情況,依據統計數據制成如下的統計圖表:
甲、乙兩班學生購買午餐的情況統計表
品種 | A | B | C | D |
甲 | 6 | 22 | 16 | 6 |
乙 | ? | 13 | 25 | 3 |

(1)求乙班學生人數;
(2)求乙班購買午餐費用的中位數;
(3)已知甲、乙兩班購買午餐費用的平均數為4.44元,從平均數和眾數的角度解答,哪個班購買的午餐價格較高?
(4)從這次接受調查的學生中,隨機抽查一人,恰好是購買C種午餐的學生的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,OB和OC分別平分∠ABC和∠ACB,過O作DE∥BC,分別交AB、AC于點D、E,若DE=5,BD=3,則線段CE的長為( )
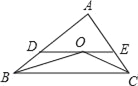
A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖1,△ABC中,BA=BC,D是平面內不與A、B、C重合的任意一點,∠ABC=∠DBE,BD=BE. 
(1)求證:△ABD≌△CBE;
(2)如圖2,當點D是△ABC的外接圓圓心時,請判斷四邊形BDCE的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明的父母出去散步,從家走了20分鐘到一個離家900米的報亭,母親隨即按原速度返回家,父親在報亭看了10分鐘報紙后,用15分鐘返回家,則表示父親、母親離家距離與時間之間的關系是(只需填序號). 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com