
【題目】如圖,在△ABC中,∠ABC=90°,以BC為直徑作⊙O,交AC于D.E為![]() 的中點,連接CE,BE,BE交AC于F.
的中點,連接CE,BE,BE交AC于F.
(1)求證:AB=AF;
(2)若AB=3,BC=4,求CE的長.

【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:(1)先證明∠EBC=∠ECF, 再證明∠ABF=∠AFB,即可得AB=AF;
(2)先應用勾股定理求出AC的長,用AC-AF求出CF的長,再應用△EFC∽△ECB可求出CE的長.
試題解析:解:(1)證明:∵BC直徑為⊙O的直徑,∴∠BEC=90°,∴∠ECF+∠EFC=90°.
∵∠ABC=90°,∴∠ABF+∠EBC=90°.又∵E為![]() 的中點,∴∠EBC=∠ECF,∴∠EFC=∠ABF.又∵∠AFB=∠EFC,∴∠AFB=∠ABF,∴AB=AF;
的中點,∴∠EBC=∠ECF,∴∠EFC=∠ABF.又∵∠AFB=∠EFC,∴∠AFB=∠ABF,∴AB=AF;
(2)∵∠ABC=90°,∴AC=![]() =
=![]() =5.又∵AB=AF=3,∴CF=AC-AF=5-3=2.∵∠EBC=∠ECF,∠E=∠E,∴△EFC∽△ECB.∴
=5.又∵AB=AF=3,∴CF=AC-AF=5-3=2.∵∠EBC=∠ECF,∠E=∠E,∴△EFC∽△ECB.∴![]() .∴BE=2CE.∵∠BEC=90°,∴
.∴BE=2CE.∵∠BEC=90°,∴![]() ,∴
,∴![]() ,∴CE=
,∴CE=![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知直線y=﹣x+4與兩坐標軸分別相交于點A,B兩點,點C是線段AB上任意一點,過C分別作CD⊥x軸于點D,CE⊥y軸于點E.雙曲線 ![]() 與CD,CE分別交于點P,Q兩點,若四邊形ODCE為正方形,且
與CD,CE分別交于點P,Q兩點,若四邊形ODCE為正方形,且 ![]() ,則k的值是( )
,則k的值是( )
A.4
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
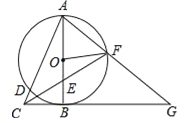
【題目】如圖,以Rt△ABC的直角邊AB為直徑作⊙O,交斜邊AC于點D,點E為OB的中點,連接CE并延長交⊙O于點F,點F恰好落在![]() 的中點,連接AF并延長與CB的延長線相交于點G,連接OF.
的中點,連接AF并延長與CB的延長線相交于點G,連接OF.
(1)求證:OF=![]() BG;
BG;
(2)若AB=4,求DC的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
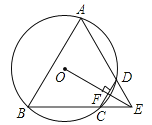
【題目】如圖,四邊形ABCD是⊙O的內(nèi)接四邊形,BC的延長線與AD的延長線交于點E,且DC=DE.
(1)求證:∠A=∠AEB;
(2)連接OE,交CD于點F,OE⊥CD,求證:△ABE是等邊三角形.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在數(shù)軸上表示下列各數(shù):0,–2.5, ![]() ,–2,+5,
,–2,+5, ![]() .并用“<”連接各數(shù).比較大小: < < < < <
.并用“<”連接各數(shù).比較大小: < < < < <
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在一個不透明的箱子里裝有紅色、藍色、黃色的球共20個,除顏色外,形狀、大小、質(zhì)地等完全相同,小明通過多次摸球?qū)嶒灪蟀l(fā)現(xiàn)摸到紅色、黃色球的頻率分別穩(wěn)定在20%和35%,則箱子里藍色球的個數(shù)很可能是______個.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com