
【題目】如圖,已知在△ABC中,AB=AC,∠B=∠C,BC=12厘米,點D為AB上一點且BD=8厘米,點P在線段BC上以2厘米/秒的速度由B點向C點運動,設運動時間為t,同時,點Q在線段CA上由C點向A點運動.
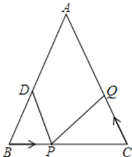
(1)用含t的式子表示PC的長為 ;
(2)若點Q的運動速度與點P的運動速度相等,當t=2時,△BPD與△CQP是否全等,請說明理由;
(3)若點Q的運動速度與點P的運動速度不相等,請求出點Q的運動速度是多少時,能夠使△BPD與△CQP全等?
【答案】(1)(12﹣2t)cm;(2)全等,理由詳見解析;(3)點Q的運動速度是![]() 厘米/秒時,能夠使三角形BPD與三角形CQP全等.
厘米/秒時,能夠使三角形BPD與三角形CQP全等.
【解析】
(1)先表示出BP,然后利用PC=BC﹣BP即可得到答案;
(2)利用速度時間與路程的關系,分別求出兩個三角形中的邊的長度,再利用SAS判定兩個三角形全等;
(3)根據全等三角形應滿足的條件探究邊之間的關系,再根據路程公式,先求得P點的運動時間,再求Q得運動速度.
解:(1)BP=2t,則PC=BC﹣BP=12﹣2t;
故答案為(12﹣2t)cm.
(2)當t=2時,BP=CQ=2×2=4厘米,
∵BD=8厘米.
又∵PC=BC﹣BP,BC=12厘米,
∴PC=12﹣4=8厘米,
∴PC=BD,
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,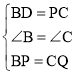 ,
,
∴△BPD≌△CQP(SAS);
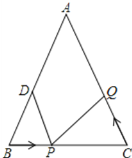
③∵vP≠vQ,
∴BP≠CQ,
又∵△BPD≌△CPQ,∠B=∠C,
∴BP=PC=6cm,CQ=BD=8cm,
∴點P,點Q運動的時間t=![]() =
=![]() =3秒,
=3秒,
∴VQ=![]() =
=![]() 厘米/秒.
厘米/秒.
即點Q的運動速度是![]() 厘米/秒時,能夠使三角形BPD與三角形CQP全等.
厘米/秒時,能夠使三角形BPD與三角形CQP全等.


 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案科目:初中數學 來源: 題型:
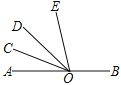
【題目】如圖,已知O為直線AB上一點,OC平分∠AOD,∠BOD=4∠DOE,∠COE=α,則∠BOE的度數為___________.(用含α的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小組做“用頻率估計概率”的試驗時,統計了某一結果出現的頻率,繪制了如圖所示的折線統計圖,則符合這一結果的試驗最有可能的是( )

A. 在“石頭、剪刀、布”的游戲中,小明隨機出的是“剪刀”
B. 一副去掉大小王的普通撲克牌洗勻后,從中任抽一張牌的花色是紅桃
C. 暗箱中有1個紅球和2個黃球,它們只有顏色上的區別,從中任取一球是黃球
D. 擲一個質地均勻的正六面體骰子,向上的面點數是4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:二次函數y=-x2+bx+c的圖象過點(-1,-8),(0,-3).
(1)求此二次函數的表達式,并用配方法將其化為y=a(x-h)2+k的形式;
(2)用五點法畫出此函數圖象的示意圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,BD、CD分別是△ABC兩個內角∠ABC、∠ACB的平分線.
①若∠A=70°,求∠BDC的度數.
②∠A=α,請用含有α的代數式表示∠BDC的度數.(直接寫出答案)
(2)如圖2,BE、CE分別是△ABC兩個外角∠MBC、∠NCB的平分線.若∠A=α,請用含有α的代數式表示∠BEC的度數.
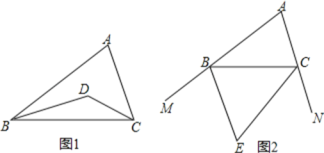
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛貨車從超市出發,向東行駛了![]() 千米到達小彬家,繼續向東行駛了
千米到達小彬家,繼續向東行駛了![]() 千米到達小穎家,然后向西行駛了
千米到達小穎家,然后向西行駛了![]() 千米到達小明家,最后回到超市.
千米到達小明家,最后回到超市.
(1)以超市為原點,向東為正,以![]() 個單位長度表示
個單位長度表示![]() ,在數軸上表示出上述各地點的位置.
,在數軸上表示出上述各地點的位置.
(2)請列式計算小明家在超市什么方向?距超市多遠?
(3)若貨車每千米油耗![]() 升,這輛貨車共耗油多少升?
升,這輛貨車共耗油多少升?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】陳老師為了解七班![]() 同學對新聞、體育、娛樂、動畫四類電視節目的喜歡情況,調查了全班
同學對新聞、體育、娛樂、動畫四類電視節目的喜歡情況,調查了全班![]() 名同學(每名同學必選且只能選擇這四類節目中的一類),并將調查結果繪制成如下不完整的條形統計圖和扇形統計圖.根據兩圖提供的信息,解答下列問題:
名同學(每名同學必選且只能選擇這四類節目中的一類),并將調查結果繪制成如下不完整的條形統計圖和扇形統計圖.根據兩圖提供的信息,解答下列問題:

![]() 求喜歡娛樂節目的人數,并將條形統計圖補充完整;
求喜歡娛樂節目的人數,并將條形統計圖補充完整;
![]() 求扇形統計圖中喜歡體育節目的人數占全班人數的百分比和圓心角
求扇形統計圖中喜歡體育節目的人數占全班人數的百分比和圓心角![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個有理數與無理數的和為無理數,任意一個不為零的有理數與一個無理數的積為無理數,而零與無理數的積為零.由此可得:如果mx+n=0,其中m、n為有理數,x為無理數,那么m=0且n=0.
(1)如果![]() ,其中a、b為有理數,那么a= ,b= .
,其中a、b為有理數,那么a= ,b= .
(2)如果![]() ,其中a、b為有理數,求a+2b的值.
,其中a、b為有理數,求a+2b的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ABC和∠ACB的外角平分線BP,CP交于點P,PE⊥AC于點E,若S△BPC=3、PE=2,S△ABC=5,求△ABC的周長是______.
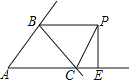
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com