
【題目】已知![]() 是二次函數,且函數圖象有最高點.
是二次函數,且函數圖象有最高點.
(1)求k的值;
(2)求頂點坐標和對稱軸,并說明當x為何值時,y隨x的增大而減少.
【答案】(1)k=﹣3;(2)當k=﹣3時,y=﹣x2頂點坐標(0,0),對稱軸為y軸,當x>0時,y隨x的增大而減少.
【解析】試題分析:(1)根據二次函數的定義得出k2+k﹣4=2,再利用函數圖象有最高點,得出k+2<0,即可得出k的值;
(2)利用(1)中k的值得出二次函數的解析式,利用形如y=ax2(a≠0)的二次函數頂點坐標為(0,0),對稱軸是y軸即可得出答案.
試題解析:解:(1)∵![]() 是二次函數,∴k2+k﹣4=2且k+2≠0,解得k=﹣3或k=2.∵函數有最高點,∴拋物線的開口向下,∴k+2<0,解得k<﹣2,∴k=﹣3;
是二次函數,∴k2+k﹣4=2且k+2≠0,解得k=﹣3或k=2.∵函數有最高點,∴拋物線的開口向下,∴k+2<0,解得k<﹣2,∴k=﹣3;
(2)當k=﹣3時,二次函數為y=﹣x2,頂點坐標為(0,0),對稱軸為y軸,當x>0時,y隨x的增大而減少.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源: 題型:
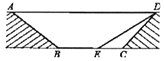
【題目】為緩解交通擁堵,某區擬計劃修建一地下通道,該通道一部分的截面如圖所示(圖中地面![]() 與通道
與通道![]() 平行),通道水平寬度
平行),通道水平寬度![]() 為8米,
為8米, ![]() ,通道斜面
,通道斜面![]() 的長為6米,通道斜面
的長為6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的長為 米;
的長為 米;
(2)為增加市民行走的舒適度,擬將設計圖中的通道斜面![]() 的坡度變緩,修改后的通道斜面
的坡度變緩,修改后的通道斜面![]() 的坡角為30°,求此時
的坡角為30°,求此時![]() 的長.(結果保留根號)
的長.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,AB為⊙O的直徑,AD與⊙O相切于點A,DE與⊙O相切于點E,點C為DE延長線上一點,且CE=CB.
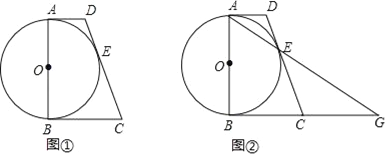
(1)求證:BC為⊙O的切線;
(2)連接AE并延長與BC的延長線交于點G(如圖②所示).若AB=![]() ,CD=9,求線段BC和EG的長.
,CD=9,求線段BC和EG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△CDE和△AOB是兩個等腰直角三角形,∠CDE=∠AOB=90°,DC=DE=1,OA=OB=a(a>1).
(1)將△CDE的頂點D與點O重合,連接AE,BC,取線段BC的中點M,連接OM.
①如圖1,若CD,DE分別與OA,OB邊重合,則線段OM與AE有怎樣的數量關系?請直接寫出你的結果;
②如圖2,若CD在△AOB內部,請你在圖2中畫出完整圖形,判斷OM與AE之間的數量關系是否有變化?寫出你的猜想,并加以證明;
③將△CDE繞點O任意轉動,寫出OM的取值范圍(用含a式子表示);
(2)是否存在邊長最大的△AOB,使△CDE的三個頂點分別在△AOB的三條邊上(都不與頂點重合)?如果存在,請你畫出此時的圖形,并求出邊長a的值;如果不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
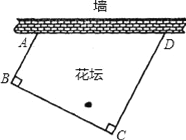
【題目】小區要用籬笆圍成一個四邊形花壇、花壇的一邊利用足夠長的墻,另三邊所用的籬笆之和恰好為18米.圍成的花壇是如圖所示的四邊形ABCD,其中∠ABC=∠BCD=90°,且BC=2AB.設AB邊的長為x米.四邊形ABCD面積為S平方米.
(1)請直接寫出S與x之間的函數關系式(不要求寫出自變量x的取值范圍).
(2)當x是多少時,四邊形ABCD面積S最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
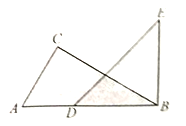
【題目】如圖所示,A,E,F,C在一條直線上,AE=CF,過E,F分別作DE⊥AC,BF⊥AC,垂足分別為E、F,且AB=CD.

(1)△ABF與△CDE全等嗎?為什么?
(2)求證:EG=FG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一副三角板的三個內角分別是![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,按如圖所示疊放在一起(點
,按如圖所示疊放在一起(點![]() 在同一直線上),若固定
在同一直線上),若固定![]() ,將
,將![]() 繞著公共頂點
繞著公共頂點![]() 順時針旋轉
順時針旋轉![]() 度(
度(![]() ),當邊
),當邊![]() 與
與![]() 的某一邊平行時,相應的旋轉角
的某一邊平行時,相應的旋轉角![]() 的值為_______.
的值為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中, ![]() 為
為![]() 邊上一點,過點
邊上一點,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為折線,將
為折線,將![]() 翻折,設所得的
翻折,設所得的![]() 與梯形
與梯形![]() 重疊部分的面積為
重疊部分的面積為![]() .
.
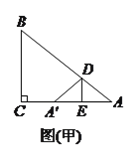
(![]() )如圖(甲),若
)如圖(甲),若![]() ,
, ![]() ,
, ![]() ,
, ![]() ,則
,則![]() 的值為__________.
的值為__________.
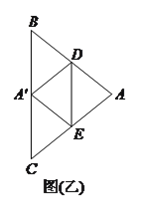
(![]() )如圖(乙),若
)如圖(乙),若![]() ,
, ![]() ,
, ![]() 為
為![]() 中點,則
中點,則![]() 的值為__________.
的值為__________.
(![]() )若
)若![]() ,
, ![]() ,
, ![]() ,設
,設![]() .
.
①求![]() 與
與![]() 的函數解析式.
的函數解析式.
②![]() 是否有最大值,若有,求出
是否有最大值,若有,求出![]() 的最大值;若沒有,請說明理由.
的最大值;若沒有,請說明理由.
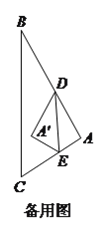
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一般情況下![]() 不成立,但有些數可以使得它成立,例如:a=b=0.我們稱使得
不成立,但有些數可以使得它成立,例如:a=b=0.我們稱使得![]() 成立的一對數a,b為“和諧數對”,記為(a,b).
成立的一對數a,b為“和諧數對”,記為(a,b).
(1)若(3,x)是“和諧數對”,求x的值;
(2)若(m,n)是“和諧數對”,求代數式![]() 的值;
的值;
(3)有一個“和諧數對”(a,b),滿足a-b=1,求a,b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com