
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求證:無論![]() 為任何實數,此方程總有兩個實數根;
為任何實數,此方程總有兩個實數根;
(2)若方程的兩個實數根為![]() 、
、![]() ,滿足
,滿足![]() ,求
,求![]() 的值;
的值;
(3)若![]() △
△![]() 的斜邊為5,另外兩條邊的長恰好是方程的兩個根
的斜邊為5,另外兩條邊的長恰好是方程的兩個根![]() 、
、![]() ,求
,求![]()
![]() 的內切圓半徑.
的內切圓半徑.
【答案】(1)詳見解析;(2)2;(3)1
【解析】
(1)將二次項系數,一次項系數,常數項分別代入根的判別式△中,并進行整理,可得![]() ,恒大于等于0,故此一元二次方程無論
,恒大于等于0,故此一元二次方程無論![]() 為任何實數時,此方程總有兩個實數根
為任何實數時,此方程總有兩個實數根
(2)根據根與系數的關系可知![]() ,
,![]() ,將
,將![]() 進行分式的加法,再將
進行分式的加法,再將![]() ,
,![]() 代入即可求得k.
代入即可求得k.
(3)解一元二次方程可得![]() ,
,![]() ,由題意
,由題意![]() △
△![]() 的斜邊為5,通過勾股定理可求得,k=4,根據直角三角形中的內切圓半徑為r=(a+b-c)/2 (a,b為直角邊,c為斜邊),代入即可求得半徑.
的斜邊為5,通過勾股定理可求得,k=4,根據直角三角形中的內切圓半徑為r=(a+b-c)/2 (a,b為直角邊,c為斜邊),代入即可求得半徑.
(1)證明:∵![]() ,
,
![]() 無論
無論![]() 為任何實數時,此方程總有兩個實數根.
為任何實數時,此方程總有兩個實數根.
(2)由題意得:![]() ,
,![]() ,
,
![]()
![]()
即![]() ,
,
解得:![]() ;
;
(3)解:
解方程得:![]() ,
,![]()
根據題意得:![]() ,即
,即![]()
設直角三角形![]() 的內切圓半徑為
的內切圓半徑為![]() ,如圖,
,如圖,
由切線長定理可得:![]() ,
,
![]() 直角三角形
直角三角形![]() 的內切圓半徑
的內切圓半徑![]() =
=![]() ;
;


科目:初中數學 來源: 題型:
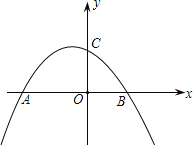
【題目】如圖,拋物線![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C
(1)求點A、B的坐標;
(2)設D為已知拋物線的對稱軸上的任意一點,當△ACD的面積等于△ACB的面積時,求點D的坐標;
(3)若直線l過點E(4,0),M為直線l上的動點,當以A、B、M為頂點所作的直角三角形有且只有三個時,求直線l的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,D為AB的中點,以CD為直徑的⊙O分別交AC,BC于點E,F兩點,過點F作FG⊥AB于點G.

(1)試判斷FG與⊙O的位置關系,并說明理由;
(2)若AC=6,CD=5,求FG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學在利用描點法畫二次函數y=ax2+bx+c(a=0)的圖象時,先取自變量x的一些值,計算出相應的函數值y,如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣3 | 0 | ﹣1 | 0 | 3 | … |
接著,他在描點時發現,表格中有一組數據計算錯誤,他計算錯誤的一組數據是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
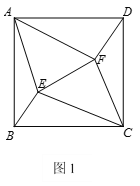
【題目】在四邊形ABCD中,AB=AD,CB=CD,∠ABC=∠ADC=90°,∠BAD=α,∠BCD=β,點E,F是四邊形ABCD內的兩個點,滿足∠EAF=![]() ,∠ECF=
,∠ECF=![]() ,連接BE,EF,FD.
,連接BE,EF,FD.
(1)如圖1,當α=β時,判斷∠ABE和∠ADF之間的數量關系,并證明你的猜想;
(2)當α≠β時,用等式表示線段BE,EF,FD之間的數量關系(直接寫出即可)
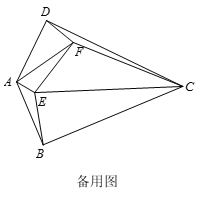
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學現有的五個社團:![]() .文學,
.文學,![]() .辯論,
.辯論,![]() .體育,
.體育,![]() .奧數,
.奧數,![]() .圍棋,為了選出“你最喜愛的社團”,在部分同學中開展了調查( 每名被調查的同學必須且只能選出一個社團),并將調查結果進行了統計,繪制了如下兩幅不完整的統計圖:
.圍棋,為了選出“你最喜愛的社團”,在部分同學中開展了調查( 每名被調查的同學必須且只能選出一個社團),并將調查結果進行了統計,繪制了如下兩幅不完整的統計圖:
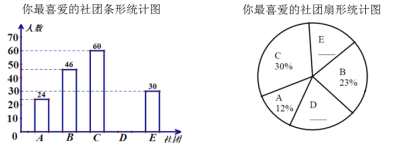
![]() 求本次被調查的人數;
求本次被調查的人數;
![]() 將上面兩幅統計圖補充完整;
將上面兩幅統計圖補充完整;
![]() 若該學校大約有學生
若該學校大約有學生![]() 人,請你估計喜歡體育社團的人數;
人,請你估計喜歡體育社團的人數;
![]() 學校為社團安排了
學校為社團安排了![]() 號教室供社團活動使用,文學設社和辯論社使用的教室恰好相鄰的概率是多少?
號教室供社團活動使用,文學設社和辯論社使用的教室恰好相鄰的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△A1C1C2的周長為1,作C1D1⊥A1C2于D1,在C1C2的延長線上取點C3,使D1C3=D1C1,連接D1C3,以C2C3為邊作等邊△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延長線上取點C4,使D2C4=D2C2,連接D2C4,以C3C4為邊作等邊△A3C3C4;…且點A1,A2,A3,…都在直線C1C2同側,如此下去,可得到△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1,則△AnCnCn+1的周長為_______(n≥1,且n為整數).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】彈簧原長(不掛重物)15cm,彈簧總長L(cm)與重物質量x(kg)的關系如下表所示:
彈簧總長L(cm) | 16 | 17 | 18 | 19 | 20 |
重物重量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
當重物質量為5kg(在彈性限度內)時,彈簧總長L(cm)是( )
A.22.5B.25C.27.5D.30
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com