
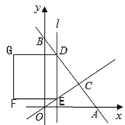
【題目】如圖,直線![]() 分別于
分別于![]() 軸、
軸、![]() 軸交于A、B兩點,與直線
軸交于A、B兩點,與直線![]() 交于點C(2,4),平行于
交于點C(2,4),平行于![]() 軸的直線
軸的直線![]() 從原點
從原點![]() 出發,以每秒1個單位長度的速度沿
出發,以每秒1個單位長度的速度沿![]() 軸向右平移,直線
軸向右平移,直線![]() 分別交直線AB、直線OC于點D、E,以DE為邊向左側作正方形DEFG,當直線
分別交直線AB、直線OC于點D、E,以DE為邊向左側作正方形DEFG,當直線![]() 經過點A時停止運動,設直線
經過點A時停止運動,設直線![]() 的運動時間為
的運動時間為![]() (秒).
(秒).
(1)![]()
(2)設線段DE的長度為![]() 求
求![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(3)當正方形DEFG的邊GF落在![]() 軸上,求出
軸上,求出![]() 的值;
的值;
(4)當![]() 時,若正方形DEFG和△OCB重疊部分面積為4,則
時,若正方形DEFG和△OCB重疊部分面積為4,則![]() 的值為________.
的值為________.
【答案】(1)b=8,k=2;(2)當t<2時,d=-4t+8;當t>2時,d=4x-8;(3)t=![]() ;(4)t=1.
;(4)t=1.
【解析】
(1)直接把點的坐標代入即可;(2)根據正方形性質和函數圖象,分兩種情況當t<2時;當t>2時;(3)設D(t,-2t+8),E(t,2t),DE=-4t+8;則 t=-4t+8;(4)由t(-4t+8)=4可得t.
解:(1)因為直線![]() 分別于
分別于![]() 軸、
軸、![]() 軸交于A、B兩點,與直線
軸交于A、B兩點,與直線![]() 交于點C(2,4),
交于點C(2,4),
所以![]() ,
,![]()
解得b=8,k=2;
(2)根據正方形性質,當t<2時,d=-4t+8;
當t>2時,d=4x-8;
(3)設D(t,-2t+8),E(t,2t),DE=-4t+8;
則 t=-4t+8,
解得t=![]() ;
;
(4)由t(-4t+8)=4,解得t=1.


科目:初中數學 來源: 題型:
【題目】某校為了解八年級學生課外閱讀情況,隨機抽取20名學生平均每周用于課外閱讀讀的時間(單位:![]() ),過程如下:
),過程如下:
(收集數據)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理數據)
課外閱讀時間 |
|
|
|
|
等級 |
|
|
|
|
人數 | 3 |
| 8 |
|
(分析數據)
平均數 | 中位數 | 眾數 |
80 |
|
|
請根據以上提供的信息,解答下列問題:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于課外讀的時間不少于![]() 為達標,該校八年級現有學生200人,估計八年級達標的學生有多少人?
為達標,該校八年級現有學生200人,估計八年級達標的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】外賣小哥騎車從商家出發,向東騎了3千米到達小林家,繼續騎2.5千米到達小紅家,然后向西騎了10千米到達小明家,最后返回商家。
(1)以商家為原點,以向東的方向為正方向,用1個單位長度表示1千米,在數軸上表示出小明家,小林家,小紅家的位置。(小林家用點A表示,小紅家用點B表示,小明家用點C表示)
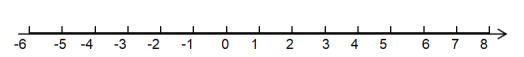
(2)小明家距小林家______千米
(3)若外賣小哥在騎車過程中每千米耗時3分鐘,那么外賣小哥在整個過程中共用時多久?(假設外賣小哥一直在勻速行駛,在每戶人家上門送外賣的時間忽略不計)
查看答案和解析>>
科目:初中數學 來源: 題型:
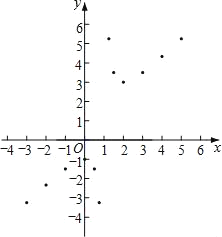
【題目】某班“數學興趣小組”對函數y=![]() +x的圖象與性質進行了探究,探究過程如下,請補充完整.
+x的圖象與性質進行了探究,探究過程如下,請補充完整.
(1)函數y=![]() +x的自變量x的取值范圍是 ;
+x的自變量x的取值范圍是 ;
(2)下表是y與x的幾組對應值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | |
|
|
| 2 | 3 | 4 | 5 | … |
y | … | ﹣ | ﹣ | ﹣ | ﹣1 | ﹣ | ﹣ |
|
| 3 |
| m |
| … |
則m= ;
(3)如圖,在平面直角坐標系xOy中,描出了以上表中各對對應值為坐標的點,根據描出的點,畫出該函數的圖象;
(4)該函數的圖象關于點( , )成中心對稱;
(5)直線y=m與該函數的圖象無交點,則m的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有如下說法:①直線是一個平角;②如果線段AB=BC,則B是線段AC的中點;③射線AB與射線BA表示同一射線;④用一個擴大2倍的放大鏡去看一個角,這個角擴大2倍;⑤兩點之間,直線最短;⑥120.5°=120°30′,其中正確的有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
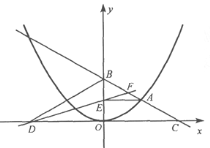
【題目】如圖,在平面直角坐標系中,A是拋物線![]() 上的一個動點,且點A在第一象限內.AE⊥y軸于點E,點B坐標為(0,2),直線AB交
上的一個動點,且點A在第一象限內.AE⊥y軸于點E,點B坐標為(0,2),直線AB交![]() 軸于點C,點D與點C關于y軸對稱,直線DE與AB相交于點F,連結BD.設線段AE的長為m,△BED的面積為S.
軸于點C,點D與點C關于y軸對稱,直線DE與AB相交于點F,連結BD.設線段AE的長為m,△BED的面積為S.
(1)當![]() 時,求S的值.
時,求S的值.
(2)求S關于![]() 的函數解析式.
的函數解析式.
(3)①若S=![]() 時,求
時,求![]() 的值;
的值;
②當m>2時,設![]() ,猜想k與m的數量關系并證明.
,猜想k與m的數量關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC是等邊三角形,點D、E分別在邊BC、AC上,且CD=CE,連接DE并延長至點F,使EF=AE,連接AF,CF,連接BE并延長交CF于點G.下列結論:
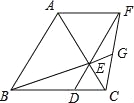
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,則GF=2EG.其中正確的結論是 .(填寫所有正確結論的序號)
【答案】①②③④.
【解析】
試題分析:①由△ABC是等邊三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等邊三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等邊三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正確.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四邊形ABDF是平行四邊形,所以DF=AB=BC,故②正確.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正確.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正確.
=2,即FG=2EG.故④正確.
考點:三角形綜合題.
【題型】填空題
【結束】
19
【題目】先化簡,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,D、F是AB邊上的兩點,以DF為直徑的⊙O與BC相交于點E,連接EF,過F作FG⊥BC于點G,其中∠OFE=![]() ∠A.
∠A.
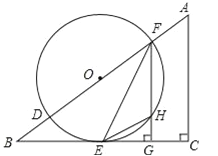
(1)求證:BC是⊙O的切線;
(2)若sinB=![]() ,⊙O的半徑為r,求△EHG的面積(用含r的代數式表示).
,⊙O的半徑為r,求△EHG的面積(用含r的代數式表示).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com