
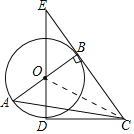
【題目】如圖,Rt△ABC中,∠ABC=90°,以AB為直徑作⊙O,點D為⊙O上一點,且CD=CB、連接DO并延長交CB的延長線于點E.
(1)判斷直線CD與⊙O的位置關系,并說明理由;
(2)若BE=4,DE=8,求AC的長.

【答案】(1)相切,證明見解析;(2)6![]() .
.
【解析】
(1)欲證明CD是切線,只要證明OD⊥CD,利用全等三角形的性質即可證明;
(2)設⊙O的半徑為r.在Rt△OBE中,根據OE2=EB2+OB2,可得(8﹣r)2=r2+42,推出r=3,由tan∠E=![]() ,推出
,推出![]() ,可得CD=BC=6,再利用勾股定理即可解決問題.
,可得CD=BC=6,再利用勾股定理即可解決問題.
(1)相切,理由如下,
如圖,連接OC,
∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD,
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切線;
(2)設⊙O的半徑為r,
在Rt△OBE中,∵OE2=EB2+OB2,
∴(8﹣r)2=r2+42,
∴r=3,AB=2r=6,
∵tan∠E=![]() ,
,
∴![]() ,
,
∴CD=BC=6,
在Rt△ABC中,AC=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,![]() ,點
,點![]() 在
在![]() 軸上,將三角形
軸上,將三角形![]() 沿
沿![]() 軸負方向平移,平移后的圖形為三角形
軸負方向平移,平移后的圖形為三角形![]() ,且點
,且點![]() 的坐標為
的坐標為![]() .
.
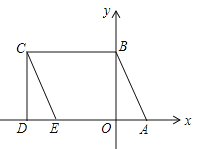
(1)直接寫出點![]() 的坐標為 ;
的坐標為 ;
(2)在四邊形![]() 中,點
中,點![]() 從點
從點![]() 出發,沿“
出發,沿“![]() ”移動,若點
”移動,若點![]() 的速度為每秒1個單位長度,運動時間為
的速度為每秒1個單位長度,運動時間為![]() 秒,回答下問題:
秒,回答下問題:
①求點![]() 在運動過程中的坐標(用含
在運動過程中的坐標(用含![]() 的式子表示,寫出過程);
的式子表示,寫出過程);
②當![]() 秒時,點
秒時,點![]() 的橫坐標與縱坐標互為相反數;
的橫坐標與縱坐標互為相反數;
③當![]() 秒
秒![]() 秒時,設
秒時,設![]() ,
,![]() ,
,![]() ,試問
,試問![]() 之間的數量關系能否確定?若能,請用含
之間的數量關系能否確定?若能,請用含![]() 的式子表式
的式子表式![]() ,寫出過程;若不能,說明理由.
,寫出過程;若不能,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
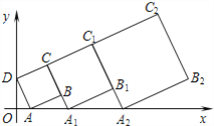
【題目】在平面坐標系中,正方形ABCD的位置如圖所示,點A的坐標為(1,0),點D的坐標為(0,2),延長CB交x軸于點A1,作正方形A1B1C1C,延長C1B1交x軸于點A2,作正方形A2B2C2C1,………按這樣的規律進行下去,正方形A2018B2018C2018C2017的面積為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
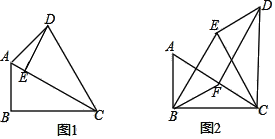
【題目】在Rt△ABC中,∠ABC=90°,∠ACB=30°,將△ABC繞點C順時針旋轉一定的角度![]() 得到△DEC,點A、B的對應點分別是D、E.
得到△DEC,點A、B的對應點分別是D、E.
(1)當點E恰好在AC上時,如圖1,求∠ADE的大小;
(2)若![]() =60°時,點F是邊AC中點,如圖2,求證:DF=BE
=60°時,點F是邊AC中點,如圖2,求證:DF=BE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】撫順市某校想知道學生對“遙遠的赫圖阿拉”,“旗袍故里”等家鄉旅游品牌的了解程度,隨機抽取了部分學生進行問卷調查,問卷有四個選項(每位被調查的學生必選且只選一項)A.十分了解,B.了解較多,C.了解較少,D.不知道.將調查的結果繪制成如下兩幅不完整的統計圖,請根據兩幅統計圖中的信息回答下列問題:
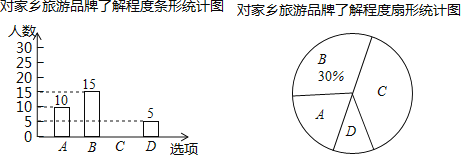
(1)本次調查了多少名學生?
(2)補全條形統計圖;
(3)該校共有500名學生,請你估計“十分了解”的學生有多少名?
(4)在被調查“十分了解”的學生中有四名學生會干部,他們中有3名男生和1名女生,學校想從這4人中任選兩人做家鄉旅游品牌宣傳員,請用列表或畫樹狀圖法求出被選中的兩人恰好是一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店計劃購進![]() 兩種計算器若購進A計算器10個,B計算器5個,需要1000元:若購進A計算器5個,B計算器3個,需要550元.
兩種計算器若購進A計算器10個,B計算器5個,需要1000元:若購進A計算器5個,B計算器3個,需要550元.
(1)購進A、B兩種計算器每個各需多少元?
(2)該商店決定購進這兩種計算器180個,若購進A種計算器的數量不少于B種計算器數量的6倍,且不超過B種計算器數量的8倍,則該商店共有幾種進貨方案?
(3)若銷售每個A計算器可獲利潤20元,每個B計算器可獲利潤30元,在(2)的各種進貨方案中,哪一種方案獲利潤較大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市合江縣先灘鄉出產的香米口感香糯,包裝質量為每袋![]() 千克,縣糧油公司應成都某糧油公司要求抽取
千克,縣糧油公司應成都某糧油公司要求抽取![]() 袋樣品進行檢測,稱重結果如下表(單位:千克):
袋樣品進行檢測,稱重結果如下表(單位:千克):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)為了簡化運算,可選取一個恰當的基準數_________,用正、負數填寫下表:
原質量 |
|
|
|
|
|
|
|
|
|
|
與基準數的差距 |
(2)根據這個表,計算這![]() 袋先灘香米的總質量.
袋先灘香米的總質量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程(k﹣2)2x2+(2k+1)x+1=0有實數解,且反比例函數y=![]() 的圖象經過第二、四象限,若k是常數,則k的值為( )
的圖象經過第二、四象限,若k是常數,則k的值為( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
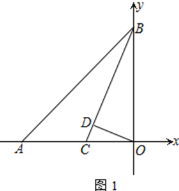
【題目】如圖,A(-t,0)、B(0,t),其中t>0,點C為OA上一點,OD⊥BC于點D,且∠BCO=45°+∠COD
(1) 求證:BC平分∠ABO
(2) 求![]() 的值
的值
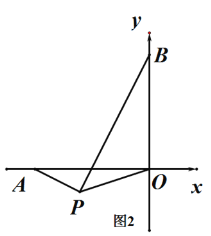
(3) 若點P為第三象限內一動點,且∠APO=135°,試問AP和BP是否存在某種確定的位置關系?說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com