
【題目】如圖,已知點A(4,0),B(0,4![]() ),把一個直角三角尺DEF放在△OAB內,使其斜邊FD在線段AB上,三角尺可沿著線段AB上下滑動.其中∠EFD=30°,ED=2,點G為邊FD的中點.
),把一個直角三角尺DEF放在△OAB內,使其斜邊FD在線段AB上,三角尺可沿著線段AB上下滑動.其中∠EFD=30°,ED=2,點G為邊FD的中點.
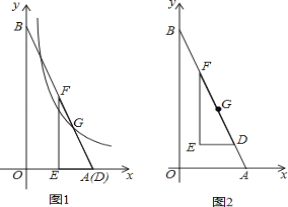
(1)求直線AB的解析式;
(2)如圖1,當點D與點A重合時,求經過點G的反比例函數y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑動的過程中,經過點G的反比例函數的圖象能否同時經過點F?如果能,求出此時反比例函數的解析式;如果不能,說明理由.
【答案】(1)y=-![]() x+4
x+4![]() ;(2)y=
;(2)y=![]() ;(3)y=
;(3)y=![]() .
.
【解析】
試題分析:(1)設直線AB的解析式為y=kx+b,把點A、B的坐標代入,組成方程組,解方程組求出k、b的值即可;
(2)由Rt△DEF中,求出EF、DF,在求出點D坐標,得出點F、G坐標,把點G坐標代入反比例函數求出k即可;
(3)設F(t,-![]() t+4
t+4![]() ),得出D、G坐標,設過點G和F的反比例函數解析式為y=
),得出D、G坐標,設過點G和F的反比例函數解析式為y=![]() ,用待定系數法求出t、m,即可得出反比例函數解析式.
,用待定系數法求出t、m,即可得出反比例函數解析式.
試題解析:(1)設直線AB的解析式為y=kx+b,
∵A(4,0),B(0,4![]() ),
),
∴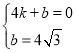 ,
,
解得: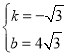 ,
,
∴直線AB的解析式為:y=-![]() x+4
x+4![]() ;
;
(2)∵在Rt△DEF中,∠EFD=30°,ED=2,
∴EF=2![]() ,DF=4,
,DF=4,
∵點D與點A重合,
∴D(4,0),
∴F(2,2![]() ),
),
∴G(3,![]() ),
),
∵反比例函數y=![]() 經過點G,
經過點G,
∴k=3![]() ,
,
∴反比例函數的解析式為:y=![]() ;
;
(3)經過點G的反比例函數的圖象能同時經過點F;理由如下:
∵點F在直線AB上,
∴設F(t,-![]() t+4
t+4![]() ),
),
又∵ED=2,
∴D(t+2,-![]() t+2
t+2![]() ),
),
∵點G為邊FD的中點.
∴G(t+1,-![]() t+3
t+3![]() ),
),
若過點G的反比例函數的圖象也經過點F,
設解析式為y=![]() ,
,
則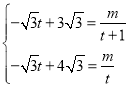 ,
,
整理得:(-![]() t+3
t+3![]() )(t+1)=(-
)(t+1)=(-![]() t+4
t+4![]() )t,
)t,
解得:t=![]() ,
,
∴m=![]() ,
,
∴經過點G的反比例函數的圖象能同時經過點F,這個反比例函數解析式為:y=![]() .
.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:初中數學 來源: 題型:
【題目】下列說法中正確的是 ( )
A. 一次函數是正比例函數 B. 正比例函數不是一次函數
C. 不是正比例函數就不是一次函數 D. 不是一次函數就不是正比例函數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列結論錯誤的是( )
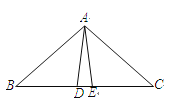
A.△ABE≌△ACD B.△ABD≌△ACE C.∠C=30° D.∠DAE=40°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】油箱中存油20升,油從油箱中均勻流出,流速為0.2升/分鐘,則油箱中剩余油量 Q(升)與流出時間t(分鐘)的函數關系是( )
A.Q=0.2t
B.Q=20﹣0.2t
C.t=0.2Q
D.t=20﹣0.2Q
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商家預測一種應季襯衫能暢銷市場,就用13 200元購進了一批這種襯衫,面市后果然供不應求,商家又用28 800元購進了第二批這種襯衫,所購數量是第一批購進量的2倍,但單價貴了10元.
(1)該商家購進的第一批襯衫是多少件?
(2)若兩批襯衫按相同的標價銷售,最后剩下50件按八折優惠賣出,如果兩批襯衫全部售完利潤率不低于25%(不考慮其他因素),那么每件襯衫的標價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用配方法解一元二次方程x2-6x+3=0時,配方得( )
A. (x+3)2=6 B. (x-3)2=6
C. (x+3)2=3 D. (x-3)2=3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com