Question

【題目】（1）問題發現

如圖1，△ACB和△DCE均為等邊三角形，點A，D，E在同一直線上，連接BE．

填空：

①∠AEB的度數為___________；

②線段AD，BE之間的數量關系為___________．

（2）拓展探究

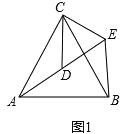
如圖2，△ACB和△DCE均為等腰直角三角形，∠ACB=∠DCE=90°，點A，D，E在同一直線上，CM為△DCE中DE邊上的高，連接BE，請判斷∠AEB的度數及線段CM，AE，BE之間的數量關系，并說明理由．

（3）解決問題

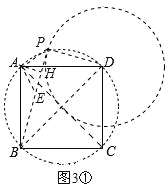
如圖3，在正方形ABCD中，CD=，若點P滿足PD=1，且∠BPD=90°，請直接寫出點A到BP的距離．

Answer 1

【答案】（1）①60°；②AD=BE；（2）∠AEB=90°，AE=BE+2CM，理由見解析；（3）或．

【解析】

試題分析：（1）①如圖1，∵△ACB和△DCE均為等邊三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=60°．∴∠ACD=∠BCE．在△ACD和△BCE中，，∴△ACD≌△BCE（SAS）．∴∠ADC=∠BEC．∵△DCE為等邊三角形，∴∠CDE=∠CED=60°．∵點A，D，E在同一直線上，∴∠ADC=120°．∴∠BEC=120°．∴∠AEB=∠BEC﹣∠CED=60°．故答案為：60°．

②∵△ACD≌△BCE，∴AD=BE．故答案為：AD=BE．

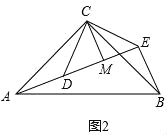
（2）∠AEB=90°，AE=BE+2CM．理由：如圖2，∵△ACB和△DCE均為等腰直角三角形，∴CA=CB，CD=CE，∠ACB=∠DCE=90°．∴∠ACD=∠BCE．在△ACD和△BCE中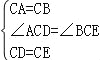，，∴△ACD≌△BCE（SAS）．∴AD=BE，∠ADC=∠BEC．∵△DCE為等腰直角三角形，∴∠CDE=∠CED=45°．∵點A，D，E在同一直線上，∴∠ADC=135°．∴∠BEC=135°．∴∠AEB=∠BEC﹣∠CED=90°．∵CD=CE，CM⊥DE，∴DM=ME．∵∠DCE=90°，∴DM=ME=CM．∴AE=AD+DE=BE+2CM．

（3）點A到BP的距離為或．理由如下：∵PD=1，∴點P在以點D為圓心，1為半徑的圓上．∵∠BPD=90°，∴點P在以BD為直徑的圓上．∴點P是這兩圓的交點．

①當點P在如圖3①所示位置時，連接PD、PB、PA，作AH⊥BP，垂足為H，過點A作AE⊥AP，交BP于點E，如圖3①．∵四邊形ABCD是正方形，∴∠ADB=45°．AB=AD=DC=BC=，∠BAD=90°．∴BD=2．∵DP=1，∴BP=．∵∠BPD=∠BAD=90°，∴A、P、D、B在以BD為直徑的圓上，∴∠APB=∠ADB=45°．∴△PAE是等腰直角三角形．又∵△BAD是等腰直角三角形，點B、E、P共線，AH⊥BP，∴由（2）中的結論可得：BP=2AH+PD．∴=2AH+1．∴AH=．

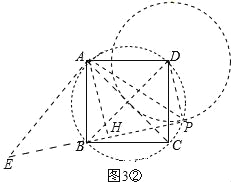
②當點P在如圖3②所示位置時，連接PD、PB、PA，作AH⊥BP，垂足為H，過點A作AE⊥AP，交PB的延長線于點E，如圖3②．同理可得：BP=2AH﹣PD．∴=2AH﹣1．∴AH=．綜上所述：點A到BP的距離為或．