黄色手机在线视频,久久久久综合一区二区三区,日韩中文字幕免费在线

精英家教網 > 初中數學 > 題目詳情

【題目】已知一次函數圖象經過點(3 ， 5) ， (－4，－9)兩點.

（1）求一次函數解析式；

（2）求這個一次函數圖象和x軸、y軸的交點坐標.

【答案】（1）直線的解析式是y=2x-1；（2）與y軸交點（0，-1），與x軸交點.

【解析】（1）設函數解析式為y=kx+b，利用待定系數法可求得k、b的值，可求得一次函數解析式；

（2）分別令x=0和y=0，可求得圖象與y軸和x軸的交點坐標．

（1）設一次函數解析式為y=kx+b（k≠0），把點（3，5），（﹣4，﹣9）分別代入解析式可得：，解得：，∴一次函數解析式為y=2x﹣1；

（2）當x=0時，y=﹣1，當y=0時，2x﹣1=0，解得：x=，∴函數圖象與坐標軸的交點為（0，﹣1），（，0）．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】現在，蘇寧商場進行促銷活動，出售一種優惠購物卡（注：此卡只作為購物優惠憑證不能頂替貨款），花300元買這種卡后，憑卡可在這家商場按標價的8折購物.

（1）顧客購買多少元金額的商品時，買卡與不買卡花錢相等？在什么情況下購物合算？

（2）小張要買一臺標價為3500元的冰箱，如何購買合算？小張能節省多少元錢？

（3）小張按合算的方案，把這臺冰箱買下，如果商場還能盈利25％，這臺冰箱的進價是多少元？

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】已知數軸上三點A，O，B表示的數分別為6，0，－4，動點P從A出發，以每秒6個單位的速度沿數軸向左勻速運動.

（1）當點P到點A的距離與點P到點B的距離相等時，點P在數軸上表示的數是；

（2）另一動點R從B出發，以每秒4個單位的速度沿數軸向左勻速運動，若點P、R同時出發，問點P運動多少時間追上點R？

（3）若M為AP的中點，N為PB的中點，點P在運動過程中，線段MN的長度是否發生變化？若發生變化，請你說明理由；若不變，請你畫出圖形，并求出線段MN的長度.

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，在△ABC中，AB=AC，∠BAC=36°，DE是線段AC的垂直平分線，若BE=a，AE=b，則用含a、b的代數式表示△ABC的周長為．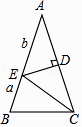

查看答案和解析>>

科目：初中數學 來源： 題型：

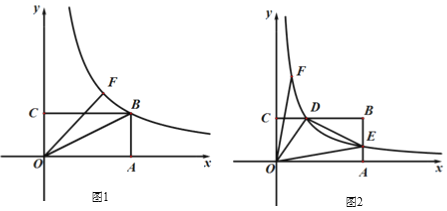
【題目】如圖，四邊形OABC為矩形，點B坐標為（4，2），A，C分別在x軸，y軸上，點F在第一象限內，OF的長度不變，且反比例函數經過點F.

（1）如圖1，當F在直線y = x上時，函數圖象過點B，求線段OF的長.

（2）如圖2，若OF從（1）中位置繞點O逆時針旋轉，反比例函數圖象與BC，AB相交，交點分別為D，E，連結OD，DE，OE.

①求證：CD=2AE.

②若AE+CD=DE，求k.

③設點F的坐標為（a，b），當△ODE為等腰三角形時，求（a+b）2的值.

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】某校為了解全校學生上學期參加“生涯規劃”社區活動的情況，學校隨機調查了本校50名學生參加社區活動的次數，并將調查所得的數據整理如下：

參加社區活動次數的頻數、頻率

活動次數x	頻數	頻率
0＜x≤3	10	0.20
3＜x≤6	a	0.24
6＜x≤9	16	0.32
9＜x≤12	6	0.12
12＜x≤15	b	m
15＜x≤18	2	n

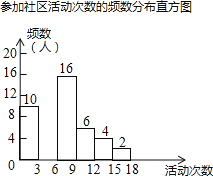
根據以上圖表信息，解答下列問題：

（1）表中a= ， b= ， m= ， n= .

（2）請把頻數分布直方圖補充完整（畫圖后請標注相應的數據）；

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖1，直線y=x+1與拋物線y=2x2相交于A、B兩點，與y軸交于點M，M、N關于x軸對稱，連接AN、BN．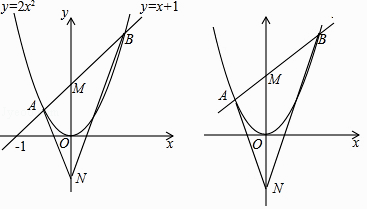

（1）①求A、B的坐標；②求證：∠ANM=∠BNM；
（2）如圖2，將題中直線y=x+1變為y=kx+b（b＞0），拋物線y=2x2變為y=ax2（a＞0），其他條件不變，那么∠ANM=∠BNM是否仍然成立？請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】我市雷雷服飾有限公司生產了一款夏季服裝，通過實體商店和網上商店兩種途徑進行銷售，銷售一段時間后，該公司對這種商品的銷售情況，進行了為期30天的跟蹤調查，其中實體商店的日銷售量y1（百件）與時間t（t為整數，單位：天）的部分對應值如下表所示，網上商店的日銷售量y2（百件）與時間t（t為整數，單位：天）的部分對應值如圖所示．

時間t（天）	0	5	10	15	20	25	30
日銷售量 y1（百件）	0	25	40	45	40	25	0

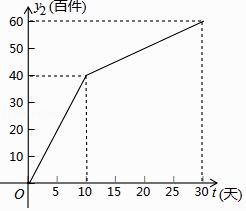
（1）請你在一次函數、二次函數和反比例函數中，選擇合適的函數能反映y1與t的變化規律，并求出y1與t的函數關系式及自變量t的取值范圍；
（2）求y2與t的函數關系式，并寫出自變量t的取值范圍；
（3）在跟蹤調查的30天中，設實體商店和網上商店的日銷售總量為y（百件），求y與t的函數關系式；當t為何值時，日銷售總量y達到最大，并求出此時的最大值．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】如圖，在平面直角坐標系中，菱形ABCD的頂點A在y軸上，且點A坐標為（0，4），BC在x軸正半軸上，點C在B點右側，反比例函數（x＞0）的圖象分別交邊AD，CD于E，F，連結BF，已知，BC=k，AE=CF，且S四邊形ABFD=20，則k= _________．

[Failed to download image : http://192.168.0.10:8086/QBM/2019/1/17/2120855162306560/2123559773659136/STEM/85e8312ee4314e6b84d61ad733d78d14.png]

查看答案和解析>>

同步練習冊答案

練習冊

高中

初中

小學