【題目】如圖，點A，B為定點，直線l∥AB，P是直線l上一動點．對于下列各值：①線段AB的長②△PAB的周長③△PAB的面積④∠APB的度數其中不會隨點P的移動而變化的是（ ）
A. 
B. 
C. 
D. 
科目：初中數學 來源： 題型：
【題目】在如圖的正方形網格中，每一個小正方形的邊長為1.格點三角形 ABC (頂點是網格線交點的三角形)的頂點 A ，C 的坐標分別是(-4 ，6) ，(-1，4) ．
(1)請在圖中的網格平面內建立平面直角坐標系；
(2)請畫出△ABC 關于 x 軸對稱的△A1B1C1 ；并直接寫出A1B1C1的坐標.
(3)請在 y 軸上求作一點 P ，使△PB1C 的周長最小，
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，拋物線y=ax2+bx﹣
與x軸交于A（1，0），B（﹣3，0）兩點，現有經過點A的直線l：y=kx+b1與y軸交于點C，與拋物線的另個交點為D．
（1）求拋物線的函數表達式；
（2）若點D在第二象限且滿足CD=5AC，求此時直線1的解析式；在此條件下，點E為直線1下方拋物線上的一點，求△ACE面積的最大值，并求出此時點E的坐標；
（3）如圖，設P在拋物線的對稱軸上，且在第二象限，到x軸的距離為4，點Q在拋物線上，若以點A，D，P，Q為頂點的四邊形能否成為平行四邊形？若能，請直接寫出點Q的坐標；若不能，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠BAC＝90°，分別以AC，BC為邊長，在三角形外作正方形ACFG和正方形BCED．若AC＝4，AB＝6，則EF＝______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：∠1＝∠2，EG平分∠AEC．
（1）如圖①，∠MAE＝45°，∠FEG＝15°，∠NCE＝75°．求證：AB∥CD；
（2）如圖②，∠MAE＝140°，∠FEG＝30°，當∠NCE＝ °時，AB∥CD；
（3）如圖②，請你直接寫出∠MAE、∠FEG、∠NCE之間滿足什么關系時，AB∥CD；
（4）如圖③，請你直接寫出∠MAE、∠FEG、∠NCE之間滿足什么關系時，AB∥CD．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】重慶八中的老師工作很忙，但初一年級很多數學老師仍然堅持鍛煉身體，比如張老師就經常堅持飯后走一走．某天晚飯后他從學校慢步到附近的中央公園，在公園里休息了一會后，因學校有事，快步趕回學校．下面能反映當天張老師離學校的距離y與時間x的關系的大致圖象是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（1）（2x﹣1）（﹣1﹣2x）；
（2）x（x﹣1）﹣（x+1）（x﹣2）；
（3）
；
（4）
；
（5）（2m﹣
n）2+（﹣2m﹣n）2；
（6）（m2﹣mn+n2）（m2+mn+n2）；
（7）（a+b）（a﹣b）+（4ab3﹣8a2b2）÷4ab；
（8）（2x﹣3y）6×（3y﹣2x）3÷（2x﹣3y）7．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠AOB＝25°，點M、N分別是邊OA、OB上的定點，點P、Q分別是邊OB、OA上的動點，記∠MPQ＝α，∠PQN＝β，當MP＋PQ＋QN最小時，則β﹣α的值為（ ）
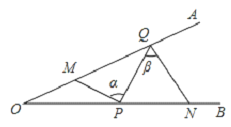
A.50°B.40°C.30°D.25°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
