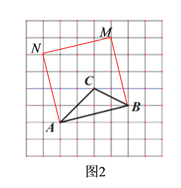
【題目】如圖，將△ABC放在每個小正方形的邊長為1的網格中，點A，點B，點C均落在格點上．
（1）計算AC2+BC2的值等于 ；
（2）請在如圖所示的網格中，用無刻度的直尺，畫出一個平行四邊形ABEF，使得該平行四邊形的面積等于16；
（3）請在如圖所示的網格中，用無刻度的直尺，畫出一個矩形ABMN，使得該矩形的面積等于AC2+BC2．
【答案】（1）13；（2）見解析（3）見解析
【解析】分析：
（1）結合圖形，由勾股定理分別計算出AC2和BC2，再求兩者的和即可；
（2）由圖可知，點A到點B的水平距離為4，結合S平行四邊形ABEF=16可知，BE=FA=4，由此即可畫出圖形如下圖1所示；
（3）由圖易得AB=
，結合S矩形ABMN= AC2+BC2=13可知AN=BM=，即矩形ABMN是正方形，由此即可畫出圖形如下圖2所示；
詳解：
（1）如圖1，∵AC2=22+22=8，BC2=22+12=5，
∴AC2+BC2=8+5=13；
（2）如下圖1所示，圖中的平行四邊形ABEF為所求平行四邊形；
（3）如下圖2所示，圖中的矩形ABMN為所求矩形；
科目：初中數學 來源： 題型：
【題目】如圖1，△ABC和△CDE都是等腰直角三角形，∠C=90°，將△CDE繞點C逆時針旋轉一個角度α（0°＜α＜90°），使點A，D，E在同一直線上，連接AD，BE．
（1）①依題意補全圖2；
②求證：AD=BE，且AD⊥BE；
③作CM⊥DE，垂足為M，請用等式表示出線段CM，AE，BE之間的數量關系；
（2）如圖3，正方形ABCD邊長為
， 若點P滿足PD=1，且∠BPD=90°，請直接寫出點A到BP的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】正方形CEDF的頂點D、E、F分別在△ABC的邊AB、BC、AC上．
（1）如圖，若tanB=2，則
的值為
（2）將△ABC繞點D旋轉得到△A′B′C′，連接BB′、CC′．若
， 則tanB的值為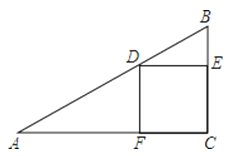 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，已知點A（3，0），B（0，4），將△BOA繞點A按順時針方向旋轉得△CDA，連接OD．當∠DOA=∠OBA時，直線CD的解析式為________
查看答案和解析>>
科目：初中數學 來源： 題型：
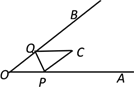
【題目】如圖，已知∠AOB＝45°，點P、Q分別是邊OA，OB上的兩點，將∠O沿PQ折疊，點O落在平面內點C處.若折疊后PC⊥QB，則∠OPQ的度數是____________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面是按一定規律排列且形式相似的一列數：
第1個數：a1＝
－(1＋
)；
第2個數：a2＝－(1＋)[1＋
][1＋
]；
第3個數：a3＝－(1＋)[1＋][1＋][1＋
](1＋
]．
(1)計算這三個數的結果(直接寫答案)：
a1＝___；a2＝___；a3＝___；
(2)請按上述規律寫出第4個數a4的形式并計算結果；
(3)請根據上述規律寫出第n (n為正整數)個數an的形式(中間部分用省略號，兩端部分必須寫詳細)，然后直接寫出計算結果．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平行四邊形ABCD繞點A逆時針旋轉30°，得到平行四邊形AB′C′D′（點B′與點B是對應點，點C′與點C是對應點，點D′與點D是對應點），點B′恰好落在BC邊上，則∠C的度數等于（ ）
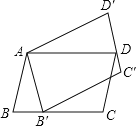
A. 100° B. 105° C. 115° D. 120°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，把一個多邊形的一個頂點與其余各頂點連接起來，可以把這個多邊形分割成若干個三角形.
（1）把一個100邊形的一個頂點與其余各頂點連接起來，一共可以連幾條線段？
（2）在（1）中，這些線段將100邊形分割成幾個三角形？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、乙兩人加工同一種機器零件，甲比乙每小時多加工10個零件，甲加工150個零件所用的時間與乙加工120個零件所用時間相等
（1）求甲、乙兩人每小時各加工多少個機器零件？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com