
【題目】觀察下列數表

根據數表反映的規律,猜想第6行與第6列的交叉點上的數應為多少.
(1)第n行與第n列的交叉點上的數應為多少.(用含正整數n的式子表示)
(2)計算左上角2×2的正方形里所有數字之和,即:![]()
![]() 在數表中任取幾個2×2的正方形,計算其中所有數字之和,歸納你得出的結論.
在數表中任取幾個2×2的正方形,計算其中所有數字之和,歸納你得出的結論.
【答案】第(1)第6行與第6列的交叉點上的數是11,第n行與第n列的交叉點上的數應為(2n﹣1);(2)四個數的和是n+(﹣n+1)+(﹣n+1)+(n﹣2)=0,結論:任取2×2的正方形上的四個數字的和都是0.
【解析】
觀察所給四行可知,第1行與第1列的交叉點上的數是1,第2行與第2列的交叉點上的數是3=2×2﹣1,第3行與第3列的交叉點上的數是5=2×3﹣1,第4行與第4列的交叉點上的數是7=2×4﹣1,據此可求出,第6行與第6列的交叉點上的數;
(1)根據前面觀察出的規律,可寫出第n行與第n列的交叉點上的數;
(2)根據所得規律,表示出四個數相加即可求出結論.
第1行與第1列的交叉點上的數是1,
第2行與第2列的交叉點上的數是3=2×2﹣1,
第3行與第3列的交叉點上的數是5=2×3﹣1,
第4行與第4列的交叉點上的數是7=2×4﹣1,
所以,第6行與第6列的交叉點上的數是2×6﹣1=11;
(1)第n行與第n列的交叉點上的數應為(2n﹣1);
(2)1+(﹣2)+(﹣2)+3=4+(﹣4)=0,
設2×2的正方形左上角的數是n(n>0),則左下角的數是﹣(n+1),右上角的數是﹣(n+1),右下角的數是(n+2),
所以,四個數的和是n﹣(n+1)﹣(n+1)+(n+2)=2n+2﹣2n﹣2=0,
設2×2的正方形左上角的數是n(n<0),則左下角的數是﹣n+1,右上角的數是﹣n+1,右下角的數是n﹣2,
所以,四個數的和是n+(﹣n+1)+(﹣n+1)+(n﹣2)=0,
結論:任取2×2的正方形上的四個數字的和都是0.


科目:初中數學 來源: 題型:
【題目】如圖,點O為原點,已知數軸上點A和點B所表示的數分別為﹣10和6,動點P從點A出發,以每秒6個單位長度的速度沿數軸正方向勻速運動,同時動點Q從點B出發,以每秒3個單位的速度沿數軸負方向勻速運動,設運動時間為t(t>0)秒
(1)當t=2時,求AP的中點C所對應的數;
(2)當PQ=OA時,求點Q所對應的數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】同學們,我們很熟悉這樣的算式:![]() ,其實,數學不僅非常美妙,而且魅力無窮.請你欣賞下列一組等式:
,其實,數學不僅非常美妙,而且魅力無窮.請你欣賞下列一組等式:
①![]()
②![]()
③![]()
④![]()
⑤……
(1)寫出第⑤個等式:![]()
(2)根據上述規律,寫出第![]() 個等式:
個等式:
![]()
(3)觀察比較,并大膽猜想:
![]()
(4)根據(2)的規律計算![]() (寫出計算過程)
(寫出計算過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某地區七年級學生對新聞、體育、動畫、娛樂、戲曲五類電視節目的喜愛情況,從該地區隨機抽取部分七年級學生作為樣本,采用問卷調查的方法收集數據(參與問卷調查的每名同學只能選擇其中一類節目),并調查得到的數據用下面的表和扇形圖來表示(表、圖都沒制作完成)
節目類型 | 新聞 | 體育 | 動畫 | 娛樂 | 戲曲 |
人數 | 36 | 90 | a | b | 27 |
根據表、圖提供的信息,解決以下問題: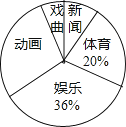
(1)計算出表中a、b的值;
(2)求扇形統計圖中表示“動畫”部分所對應的扇形的圓心角度數;
(3)若該地區七年級學生共有47500人,試估計該地區七年級學生中喜愛“新聞”類電視節目的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,BD為⊙O的直徑,BD與AC相交于點H,AC的延長線與過點B的直線相交于點E,且∠A=∠EBC.
(1)求證:BE是⊙O的切線;
(2)已知CG∥EB,且CG與BD、BA分別相交于點F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E是AB上一點,F是AD延長線上一點,且DF=BE.

(1)求證:CE=CF;
(2)若點G在AD上,且∠GCE=45°,則GE=BE+GD成立嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com