
【題目】如圖,畫![]() ,并畫
,并畫![]() 的平分線
的平分線![]() .
.
(1)將三角尺的直角頂點落在![]() 的任意一點P上,使三角尺的兩條直角邊與
的任意一點P上,使三角尺的兩條直角邊與![]() 的兩邊分別垂直,垂足為E、F(如圖1),則
的兩邊分別垂直,垂足為E、F(如圖1),則![]()
![]() (選填<,>,=)
(選填<,>,=)

(2)把三角尺繞著點P旋轉(如圖2),![]() 與
與![]() 相等嗎?試猜想
相等嗎?試猜想![]() 、
、![]() 的大小關系,并說明理由.
的大小關系,并說明理由.
拓展延伸1:在(2)條件下,過點P作直線![]() ,分別交
,分別交![]() 、
、![]() 于點G、H,如圖3
于點G、H,如圖3
①圖中全等三角形有多少對(不添加輔助線)
②猜想![]() 、
、![]() 、
、![]() 之間的關系,并證明你的猜想.
之間的關系,并證明你的猜想.
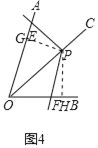
拓展延伸2:
畫![]() ,并畫
,并畫![]() 的平分線
的平分線![]() ,在
,在![]() 上任取一點P,作
上任取一點P,作![]() .
.![]() 的兩邊分別與
的兩邊分別與![]() 、
、![]() 相交于E、F兩點(如圖4),
相交于E、F兩點(如圖4),![]() 與
與![]() 相等嗎?請說明理由.
相等嗎?請說明理由.
【答案】(1)=;(2)![]() ,理由見解析;拓展延伸1:①全等三角形有3對;②
,理由見解析;拓展延伸1:①全等三角形有3對;②![]() ,理由見解析;拓展延伸2:
,理由見解析;拓展延伸2:![]() ;理由見解析;
;理由見解析;
【解析】
(1)根據角平分線的性質定理證明;
(2)證明△MPE≌△NPF,根據全等三角形的性質證明結論;
拓展延伸1:①根據等腰直角三角形的性質得到OP=PG=PH,證明△GPE≌△OPF(ASA),△EPO≌△FPH,△GPO≌△OPH,得到答案;
②根據勾股定理,全等三角形的性質解答;
拓展延伸2:作PG⊥OA于G,PH⊥OB于H,證明△PGE≌△PHF,根據全等三角形的性質證明結論.
(1)∵![]() 平分
平分![]() ,
,
∴![]() ,
,
故答案為:=;
(2)![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
由(1)得,![]() ,
,
在![]() 和
和![]() 中,
中,
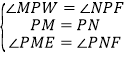 ,
,
∴![]() ,
,
∴![]() ;
;
拓展延伸1:①∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵GH⊥OC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
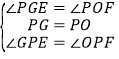 ,
,
∴![]() ,
,
同理,![]() ,
,
故答案為:3;
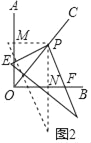
②![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ;
;
拓展延伸2:![]() ;
;
理由:作![]() 于G,
于G,![]() 于H,
于H,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
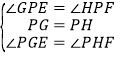 ,
,
∴![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,過點C的直線MN∥AB,D為AB邊上
一點,過點D作DE⊥BC,交直線MN于E,垂足為F,連接CD,BE.
(1)求證:CE=AD;
(2)當D在AB中點時.
①求證:四邊形BECD是菱形;
②當∠A為多少度時,四邊形BECD是正方形?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
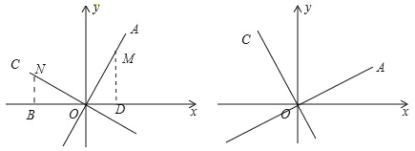
【題目】(1)問題提出:如圖已知直線OA的解析式是y=2x,OC⊥OA,求直線OC的函數解析式.
甲同學提出了他的想法:在直線y=2x上取一點M,過M作x軸的垂線,垂足為D設點M的橫坐標為m,則點M的縱坐標為2m.即OD=m,MD=2m,然后在OC上截取ON=OM,過N作x軸的垂線垂足為B.則點N的坐標為 ,直線OC的解析式為 .
(2)拓展:已知直線OA的解析式是y=kx,OC⊥OA,求直線OC的函數解析式.
(3)應用:直接寫出經過P(2,3),且垂直于直線y=﹣![]() x+2的直線解析式 .
x+2的直線解析式 .
查看答案和解析>>
科目:初中數學 來源: 題型:
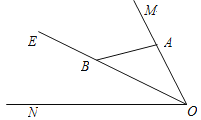
【題目】如圖,已知∠MON=80°,OE平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O重合),連接AC交射線OE于點D.當AB⊥OM,且△ADB有兩個相等的角時,∠OAC的度數為______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1)![]() -|
-|![]() -3|
-3|
(2)a3![]() 4
4![]() +(-a2)3
+(-a2)3![]() 2+(-2a4)2
2+(-2a4)2
(3)(x+2y-3)(x-2y+3)
(4)3(x-2y)2-(2x+y)(-y+2x)-3x(x-0.5y)
查看答案和解析>>
科目:初中數學 來源: 題型:
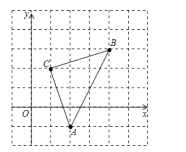
【題目】如圖,直角坐標系中,△ABC的頂點都在網格點上,其中,C點坐標為(1,2),
(1)寫出點A、B的坐標:A(_____,_____)、B(_____,_____);
(2)將△ABC先向左平移2個單位長度,再向上平移1個單位長度,得到△A′B′C′,寫出A′、B′、C′三點坐標;
(3)求△ABC的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
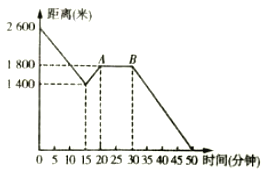
【題目】星期五小穎放學步行從學校回家,當她走了一段路后,想起要去買彩筆做畫報,于是原路返回到剛經過的文具用品店,買到彩筆后繼續往家走.如圖是她離家的距離與所用時間的關系示意圖,請根據圖中提供的信息回答下列問題:
(1)小穎家與學校的距離是 米;
(2)![]() 表示的實際意義是 ;
表示的實際意義是 ;
(3)小穎本次從學校回家的整個過程中,走的路程是多少米?
(4)買到彩筆后,小穎從文具用品店回到家步行的速度是多少米/分?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com