
【題目】如圖,四邊形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E為AB的中點.
(1)求證:AC2=ABAD;
(2)求證:CE∥AD;
(3)若AD=5,AB=7,求 ![]() 的值.
的值.
【答案】
(1)證明:∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=ABAD.
(2)證明:∵E為AB的中點,∠ACB=90°,
∴CE= ![]() AB=AE.
AB=AE.
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
∴AD∥CE
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE= ![]() AB,
AB,
∴CE= ![]() ×7=
×7= ![]() ,
,
∵AD=5,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]()
【解析】(1)首先證明△ADC∽△ACB,然后依據相似三角形的對應邊成比例得到AC2=ABAD;
(2)根據在直角三角形中,斜邊上的中線等于斜邊的一半可證得CE=![]() ,AB=AE,然后依據等邊對等角的性質可得到∠EAC=∠ECA.通過等量代換可得到∠DAC=∠ECA,故此可證明CE∥AD;
,AB=AE,然后依據等邊對等角的性質可得到∠EAC=∠ECA.通過等量代換可得到∠DAC=∠ECA,故此可證明CE∥AD;
(3)首先證明△AFD∽△CFE,然后由相似三角形的對應邊成比例的性質可求得![]() 的值.
的值.
【考點精析】解答此題的關鍵在于理解相似三角形的判定與性質的相關知識,掌握相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


科目:初中數學 來源: 題型:
【題目】(10分)如圖,ABCD中,點E,F在直線AC上(點E在F左側),BE∥DF.

(1)求證:四邊形BEDF是平行四邊形;
(2)若AB⊥AC,AB=4,BC=![]() ,當四邊形BEDF為矩形時,求線段AE的長.
,當四邊形BEDF為矩形時,求線段AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某高校共有5個大餐廳和2個小餐廳。經過測試:同時開放1個大餐廳和2個小餐廳,可供1680名學生就餐;同時開放2個大餐廳和1個小餐廳,可供2280名學生就餐。
(1)1個大餐廳和1個小餐廳分別可供多少名學生就餐?
(2)若7個餐廳同時開放,能否供全校的5300名學生就餐?請說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,點E、F分別是AD、AB的中點,EF交AC于點G,那么AG:GC的值為( )
A.1:2
B.1:3
C.1:4
D.2:3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,時鐘是我們常見的生活必需品,其中蘊含著許多數學知識.

(1)我們知道,分針和時針轉動一周都是 度,分針轉動一周是 分鐘,時針轉動一周有12小時,等于720分鐘;所以,分針每分鐘轉動 度,時針每分鐘轉動 度.
(2)從5:00到5:30,分針與時針各轉動了多少度?
(3)請你用方程知識解釋:從1:00開始,在1:00到2:00之間,是否存在某個時刻,時針與分針在同一條直線上?若不存在,說明理由;若存在,求出從1:00開始經過多長時間,時針與分針在同一條直線上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一天,媽媽下班后從公司開車回家,途中想起忘了帶第二天早上開早會的一個文件夾,于是打電話讓辦公室王阿姨馬上從公司送來,同時媽媽也往回開,遇到王阿姨后停下說了幾句話,接著繼續開車回家.設媽媽從公司出發后所用時間為t,媽媽與家的距離為s.下面能反映s與t的函數關系的大致圖象是( )
A.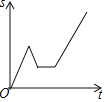 B.
B.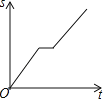
C. D.
D.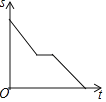
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△AOB中,兩直角邊OA,OB分別在x軸的負半軸和y軸的正半軸上,將△AOB繞點B逆時針旋轉90°后得到△A′O′B.若反比例函數 ![]() 的圖象恰好經過斜邊A′B的中點C,S△ABO=4,tan∠BAO=2,則k的值為( )
的圖象恰好經過斜邊A′B的中點C,S△ABO=4,tan∠BAO=2,則k的值為( )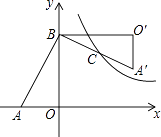
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解方程組:①![]() ②
②![]() ③
③![]() ④
④![]() ,比較適宜的方法是( )
,比較適宜的方法是( )
A.①②用代入法,③④用加減法B.①③用代入法,②④用加減法
C.②③用代入法,①④用加減法D.②④用代入法,①③用加減法
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com