
【題目】問題再現:
數形結合是一種重要的數學思想方法,借助這種思想方法可將抽象的數學知識變得直觀并且具有可操作性.初中數學里的一些代數公式,很多都可以通過表示幾何圖形面積的方法進行直觀推導和解釋.
例如:利用圖形的幾何意義驗證完全平方公式.
將一個邊長為![]() 的正方形的邊長增加
的正方形的邊長增加![]() ,形成兩個長方形和兩個正方形,如圖所示:這個圖形的面積可以表示成:
,形成兩個長方形和兩個正方形,如圖所示:這個圖形的面積可以表示成:
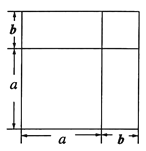
![]() 或
或![]()
∴![]()
這就驗證了兩數和的完全平方公式.
類比解決:
請你類比上述方法,利用圖形的幾何意義驗證平方差公式.
(要求畫出圖形并寫出推理過程)
問題提出:如何利用圖形幾何意義的方法證明![]() ?
?
如圖所示,![]() 表示1個1×1的正方形,即:
表示1個1×1的正方形,即:![]() ,
,![]() 表示1個2×2的正方形,
表示1個2×2的正方形,![]() 與
與![]() 恰好可以拼成1個2×2的正方形,因此:
恰好可以拼成1個2×2的正方形,因此:![]() 、
、![]() 、
、![]() 就可以表示2個2×2的正方形,即:
就可以表示2個2×2的正方形,即:![]() 而
而![]() 、
、![]() 、
、![]() 、
、![]() 恰好可以拼成一個
恰好可以拼成一個![]() 的大正方形.
的大正方形.
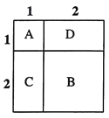
由此可得:![]() .
.
嘗試解決:
請你類比上述推導過程,利用圖形的幾何意義確定:![]() _______.(要求寫出結論并構造圖形寫出推證過程).
_______.(要求寫出結論并構造圖形寫出推證過程).
問題拓廣:
請用上面的表示幾何圖形面積的方法探究:![]() _______.(直接寫出結論即可,不必寫出解題過程).
_______.(直接寫出結論即可,不必寫出解題過程).
【答案】嘗試解決:![]() ;問題拓廣:
;問題拓廣:![]() .
.
【解析】
嘗試解決:根據規律可以利用相同的方法進行探究推證,由于是探究13+23+33=?肯定構成大正方形有9個基本圖形(3個正方形6個長方形)組成,如圖所示可以推證.
實際應用:根據規律求大正方體中含有多少個正方體,可以轉化為13+23+33+…+n3=(1+2+3+…+n)2來求得.
嘗試解決:
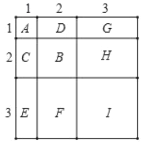
如圖,A表示1個1×1的正方形,即1×1×1=13;
B表示1個2×2的正方形,C與D恰好可以拼成1個2×2的正方形,
因此B. C. D就可以拼成2個2×2的正方形,即:2×2×2=23;
G與H、E與F和I可以拼成3個3×3的正方形,即:3×3×3=33;
而整個圖形恰好可以拼成一個(1+2+3)×(1+2+3)的大正方形,
因此可得:13+23+33=(1+2+3)2=62.
故答案為:(1+2+3)2或62.
問題拓廣:由上探究可知,13+23+33+…+n3=(1+2+3+…+n)2,
又∵1+2+3+…+n=![]()
∴13+23+33+…+n3=![]() =
=![]()
故答案為:![]()


科目:初中數學 來源: 題型:
【題目】嘉嘉和琪琪在用一副三角尺研究數學問題:
一副三角尺分別有一個角為直角,其余角度如圖1所示,![]() .
.
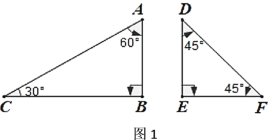
發現:
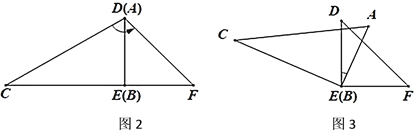
(1)如圖2,當![]() 與
與![]() 重合時,
重合時,![]() _____.
_____.
(2)如圖3,將圖2中![]() 繞
繞![]() 點順時針旋轉一定角度使得
點順時針旋轉一定角度使得![]() ,求
,求![]() 的度數.
的度數.
拓展:
(3)如圖4,繼續旋轉,使得![]() 于點
于點![]() ,
,
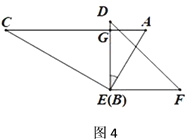
①此時![]() 與
與![]() 平行嗎?請說明理由.
平行嗎?請說明理由.
②求![]() 的度數.
的度數.
探究:
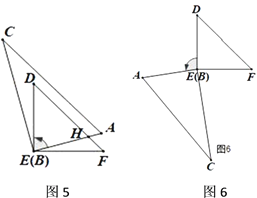
(4)如圖5、圖6,繼續旋轉,使得![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,菱形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是邊
分別是邊![]() 和
和![]() 上的點,且
上的點,且![]() .
.
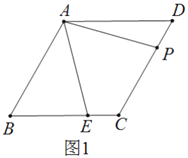
(1)求證:![]()
(2)如圖2,![]() 在
在![]() 延長線上,且
延長線上,且![]() ,求證:
,求證:![]()
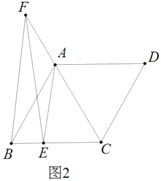
(3)如圖3,在(2)的條件下,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,求
的中點,求![]() 的長.
的長.
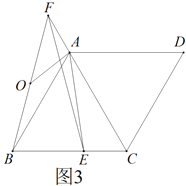
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小何按市場價格![]() 元/千克在收購了
元/千克在收購了![]() 千克蘑菇存放入冷庫中,請根據小何提供的預測信息(如圖)幫小何解決以下問題:
千克蘑菇存放入冷庫中,請根據小何提供的預測信息(如圖)幫小何解決以下問題:
(![]() )若小何想將這批蘑菇存放
)若小何想將這批蘑菇存放![]() 天后一次性出售,則
天后一次性出售,則![]() 天后這批蘑菇的銷售單價為__________元,這批蘑菇的銷售量是__________千克.
天后這批蘑菇的銷售單價為__________元,這批蘑菇的銷售量是__________千克.
(![]() )小何將這批蘑菇存放多少天后,一次性出售所得的銷售總金額為
)小何將這批蘑菇存放多少天后,一次性出售所得的銷售總金額為![]() 元?
元?
(![]() )將這批蘑菇存放多少天后一次性出售可獲得最大利潤?最大利潤是多少?
)將這批蘑菇存放多少天后一次性出售可獲得最大利潤?最大利潤是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用水平線和豎直線將平面分成若干個邊長為1的小正方形格子,小正方形的頂點,叫格點,以格點為頂點的多邊形叫格點多邊形.設格點多邊形的面積為![]() ,它各邊上格點的個數之和為
,它各邊上格點的個數之和為![]() .
.

探究一:圖中①—④的格點多邊形,其內部都只有一個格點,它們的面積與各邊上格點的個數之和的對應關系如表:
多邊形的序號 | ① | ② | ③ | ④ | … |
多邊形的面積 | 2 | 2.5 | 3 | 4 | … |
各邊上格點的個數和 | 4 | 5 | 6 | 8 | … |
![]() 與
與![]() 之間的關系式為:________.
之間的關系式為:________.
探究二:圖中⑤—⑧的格點多邊形內部都只有2個格點,請你先完善下表格的空格部分(即分別計算出對應格點多邊形的面積![]() ):
):
多邊形的序號 | ⑤ | ⑥ | ⑦ | ⑧ | … |
多邊形的面積 | … | ||||
各邊上格點的個數和 | 4 | 5 | 6 | 8 | … |
![]() 與
與![]() 之間的關系式為:________.
之間的關系式為:________.
猜想:當格點多邊形內部有且只有![]() 個格點時,
個格點時,![]() 與
與![]() 之間的關系式為:_______.
之間的關系式為:_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】聲音在空氣中的傳播速度y(m/s)隨氣溫x(℃)的變化而變化.下表給出了一組不同氣溫下聲音傳播的速度:
x(℃) | 0 | 5 | 10 | 15 | 20 | 25 |
y(m/s) | 331 | 334 | 337 | 340 | 343 | 346 |
(1)當x的值為35時,求對應的y的值;
(2)求y與x的關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】尺規作圖:作點A關于直線l的對稱點A'.
已知:直線l和l外一點A.
求作:點A關于l的對稱點A'.
作法:①在l上任取一點P,以點P為圓心,PA長為半徑作孤,交l于點B;②以點B為圓心,AB長為半徑作弧,交弧AB于點A'. 點A'就是所求作的對稱點.
由步驟①,得________
由步驟②,得________
將橫線上的內容填寫完整,并說明點A與A'關于直線l對稱的理由________.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某“欣欣”奶茶店開業大酬賓推出![]() 四款飲料.
四款飲料.![]() 千克
千克![]() 飲料的原料是
飲料的原料是![]() 千克蘋果,
千克蘋果,![]() 千克梨,
千克梨,![]() 千克西瓜;1千克
千克西瓜;1千克![]() 飲料的原料是
飲料的原料是![]() 千克蘋果,
千克蘋果,![]() 千克梨,
千克梨,![]() 千克西瓜;
千克西瓜;![]() 千克
千克![]() 飲料的原料是
飲料的原料是![]() 千克蘋果,
千克蘋果,![]() 千克梨,
千克梨, ![]() 千克西瓜;
千克西瓜;![]() 千克
千克![]() 飲料的原料是
飲料的原料是![]() 千克蘋果,
千克蘋果,![]() 千克梨,
千克梨,![]() 千克西瓜;如果每千克蘋果的成本價為
千克西瓜;如果每千克蘋果的成本價為![]() 元,每千克梨的成本價為
元,每千克梨的成本價為![]() 元,每千克西瓜的成本價為
元,每千克西瓜的成本價為![]() 元.開業當天全部售罄,銷售后,共計蘋果的總成本為
元.開業當天全部售罄,銷售后,共計蘋果的總成本為![]() 元,并且梨的總成本為
元,并且梨的總成本為![]() 元,那么西瓜的總成本為_____元
元,那么西瓜的總成本為_____元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com