
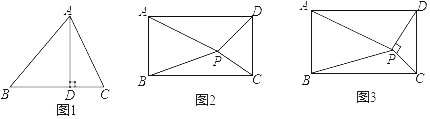
【題目】(幾何背景)如圖1,AD為銳角△ABC的高,垂足為D.求證:AB2﹣AC2=BD2﹣CD2
(知識遷移)如圖2,矩形ABCD內任意一點P,連接PA、PB、PC、PD,請寫出PA、PB、PC、PD之間的數量關系,并說明理由.
(拓展應用)如圖3,矩形ABCD內一點P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c滿足a2﹣b2=![]() c2,則
c2,則![]() 的值為 (請直接寫出結果)
的值為 (請直接寫出結果)
【答案】【幾何背景】:詳見解析;【知識遷移】:詳見解析;【拓展應用】:![]()
【解析】
幾何背景:由 Rt△ABD中,AD2=AB2﹣BD2,Rt△ACD中,AD2=AC2﹣CD2,則結論可證.
知識遷移:過P點作PE⊥AD,延長EP交BC于F,可證四邊形ABFE,四邊形DCFE是矩形.根據上面的結論求得PA、PB、PC、PD之間的數量關系.
拓展應用:根據勾股定理可列方程組,可求PD=![]() c,PC=
c,PC=![]() c即可得
c即可得![]() .
.
解:幾何背景:在Rt△ABD中,AD2=AB2﹣BD2
Rt△ACD中,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,
∴AB2﹣AC2=BD2﹣CD2.
知識遷移:BP2﹣PC2 =BF2﹣CF2.
如 圖:
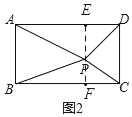
過P點作PE⊥AD,延長EP交BC于F
∴四邊形ABCD是矩形
∴AD∥BC∠BAD=∠ADC=∠DCB=∠ABC=90°
又∵PE⊥AD
∴PF⊥BC
∵PE是△APD的高
∴PA2﹣PD2=AE2﹣DE2.
∵PF是△PBC的高
∴BP2﹣PC2 =BF2﹣CF2.
∵∠BAD=∠ADC=∠DCB=∠ABC=90°,PE⊥AD,PF⊥BC
∴四邊形ABFE,四邊形DCFE是矩形
∴AE=BF,CF=DE
∴PA2﹣PD2=BP2﹣PC2.
拓展應用:∵PA2﹣PD2=BP2﹣PC2.
∴PA2﹣PB2=![]() c2.
c2.
∴PD2﹣PC2=![]() c2.
c2.
且PD2+PC2=c2.
∴PD=![]() c,PC=
c,PC=![]() c
c
∴![]() ,
,
故答案為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】一次函數y1=kx+b與y2=x+a的圖象如圖,則下列結論:①k<0;②a>0;③關于x的方程kx﹣x=a﹣b的解是x=3;④當x<3時,y1<y2中.則正確的序號有________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察圖,回答下列問題

(1)在圖①中有幾個角?
(2)在圖②中有幾個角?
(3)在圖③中有幾個角?
(4)以此類推,如圖④所示,若一個角有n條射線,此時共有多少個角?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸是一個非常重要的數學工具,通過它把數和數軸上的點建立起對應關系,揭示了數與點之間的內在聯系,也體現了“數形結合”的數學思想.如圖,數軸上的點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分別表示
分別表示![]() 、
、![]() 、0、2.5、6,請利用數軸解決下列問題:
、0、2.5、6,請利用數軸解決下列問題:
![]()
(1)數軸上,![]() 、
、![]() 兩點之間的距離是 ,
兩點之間的距離是 ,![]() 、
、![]() 兩點之間的距離是 ,到點
兩點之間的距離是 ,到點![]() 的距離是3個單位長度的點所表示的數是 .
的距離是3個單位長度的點所表示的數是 .
(2)如果將點![]() 向左移動7個單位長度,再向右移動5個單位長度,請同學們在數軸上畫出點
向左移動7個單位長度,再向右移動5個單位長度,請同學們在數軸上畫出點![]() 移動的路線圖,并指出終點所表示的數.
移動的路線圖,并指出終點所表示的數.
(3)如果點![]() 是數軸上的另一點,將點
是數軸上的另一點,將點![]() 向右移動3個單位長度,再向左移動5個單位長度,終點表示的數是
向右移動3個單位長度,再向左移動5個單位長度,終點表示的數是![]() ,那么點
,那么點![]() 表示的數是 .
表示的數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解本校九年級學生期末數學考試情況,在九年級隨機抽取了一部分學生 的期末數學成績為樣本,分為 A(90~100 分);B(80~89 分);C(60~79 分);D(0~59 分)四個等級進行統計,并將統計結果繪制成如下統計圖,請你根據統計圖解答以下 問題.
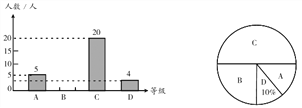
(1)這次隨機抽取的學生共有多少人?
(2)請補全條形統計圖;
(3)這個學校九年級共有學生 1200 人,若分數為 80 分(含 80 分)以上為優秀,請估 計這次九年級學生期末數學考試成績為優秀的學生人數大約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市“藝術節”期間,小明、小亮都想去觀看茶藝表演,但是只有一張茶藝表演 門票,他們決定采用抽卡片的辦法確定誰去.規則如下:
將正面分別標有數字 1、2、3、4 的四張卡片(除數字外其余都相同)洗勻后,背面朝上 放置在桌面上,隨機抽出一張記下數字后放回;重新洗勻后背面朝上放置在桌面上, 再隨機抽出一張記下數字.如果兩個數字之和為奇數,則小明去;如果兩個數字之和 為偶數,則小亮去.
(1)請用列表或畫樹狀圖的方法表示抽出的兩張卡片上的數字之和的所有可能出現 的結果;
(2)你認為這個規則公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:閱讀下列材料:已知二次三項式2x2+x+a有一個因式是(x+2),求另一個因式以及a 的值
解:設另一個因式是(2x+b),
根據題意,得2x2+x+a=(x+2)(2x+b),
展開,得2x2+x+a =2x2+(b+4)x+2b,
所以![]() ,解得
,解得![]() ,
,
所以,另一個因式是(2x3),a 的值是6.
請你仿照以上做法解答下題:已知二次三項式3x2 10x m 有一個因式是(x+4),求另一個因式以及m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
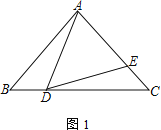
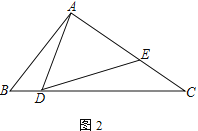
【題目】已知:△ABC中,點D為邊BC上一點,點E在邊AC上,且∠ADE=∠B
(1) 如圖1,若AB=AC,求證:![]() ;
;
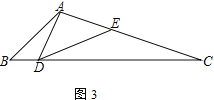
(2) 如圖2,若AD=AE,求證:![]() ;
;
(3) 在(2)的條件下,若∠DAC=90°,且CE=4,tan∠BAD=![]() ,則AB=____________.
,則AB=____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
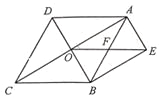
【題目】如圖,菱形ABCD的對角線AC、BD相交于點O,BE∥AC,AE∥BD,OE與AB交于點F.
(1)試判斷四邊形AEBO的形狀,并說明理由;
(2)若OE=10,AC=16,求菱形ABCD的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com