Question

【題目】為了緬懷先烈．繼承遺志，某中學初二年級同學于4月初進行“清明雁棲湖，憶先烈功垂不朽”的定向越野活動每個小組需要在點出發，跑步到點打卡（每小組打卡時間為1分鐘），然后跑步到點，……最后到達終點（假設點，點，點在一條直線上，且在行進過程中，每個小組跑步速度是不變的），“文藝組”最先出發．過了一段時間后，“方程組”開始出發，兩個小組恰好同時到達點．若“方程組”出發的時間為（單位：分鐘），在點與點之間的行進過程中，“文藝組”和“方程組”之間的距離為（單位：米），它們的函數圖像如下圖：則下面判斷不正確的是（ ）

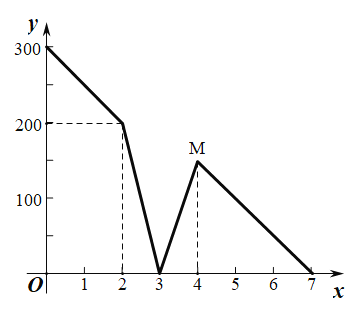
A.當時，“文藝組”恰好到達點；

B.“文藝組”的速度為150米/分鐘，“方程組”的速度為200米/分鐘他們從點出發的時間間隔為2分鐘

C.圖中點表示“方程組”在點打卡結束，開始向點出發；

D.出發點到打卡點的距離是600米，打卡點到點的距離是800米

Answer 1

【答案】D

【解析】

根據函數的圖象和已知條件分別分析探討其正確性，進一步判定得出答案即可．

A、由圖可知，當時，“文藝組”恰好到達點，正確；

B、由圖可知，“34”分鐘時，“方程組”打卡，“文藝組”一分鐘行走150米，則“文藝組”的速度為150米/分鐘；“23”分鐘時，“文藝組”打卡，“方程組”一分鐘行走200米，則“方程組”的速度為200米/分鐘，“方程組”出發前相距300米，所以從點出發的時間間隔為2分鐘，正確；

C、由圖可知，點開始“文藝組”和“方程組”之間的距離為在慢慢縮少，說明“方程組”打卡結束，在追趕“文藝組”，正確；

D、“方程組”出發點到打卡，用時3分鐘，所以AB的距離為600米，點表示“方程組”打卡結束到C點趕上“文藝組”，用時3分鐘，所以BC的距離為600米，錯誤；

正確的答案有ABC，錯誤的只有D．
故選：D．