
【題目】為了了解全校1500名學生對學校設置的籃球、羽毛球、乒乓球、踢毽子、跳繩共5項體育活動的喜愛情況,在全校范圍內隨機抽查部分學生,對他們喜愛的體育項目(每人只選一項)進行了問卷調查,將統計數據繪制成如圖兩幅不完整統計圖, 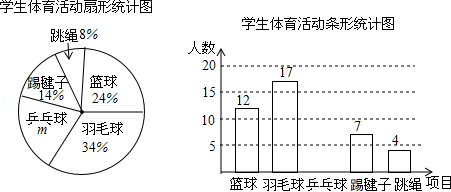
請根據圖中提供的信息解答下列各題.
(1)本次問卷調查共抽查了名學生;
(2)請補全條形統計圖;
(3)請你估計該校約有名學生最喜愛打籃球;
(4)學校準備從喜歡跳繩活動的4人(三男一女)中隨機選取2人進行體能測試,請利用列表或樹狀圖的方法,求抽到一男一女的概率.
【答案】
(1)50
(2)解:如圖所示:
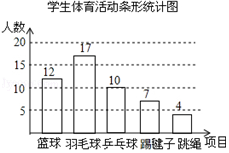
(3)360
(4)解:列表如下:
男1 | 男2 | 男3 | 女 | |
男1 | (男2,男1) | (男3,男1) | (女,男1) | |
男2 | (男1,男2) | (男3,男2) | (女,男2) | |
男3 | (男1,男3) | (男2,男3) | (女,男3) | |
女 | (男1,女) | (男2,女) | (男3,女) |
共有12種等可能的結果數,其中一男一女的情況有6種,
所以抽到一男一女的概率= ![]() =
= ![]()
【解析】解:(1)調查的總人數為12÷24%=50(人);(2)喜歡乒乓球的人數=50﹣12﹣17﹣7﹣4=10(人), 補全條形統計圖為:
⑶1500×24%=36,
所以估計該校約有360名學生最喜愛打籃球;
所以答案是50,360;
【考點精析】通過靈活運用扇形統計圖和條形統計圖,掌握能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況;能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況即可以解答此題.


科目:初中數學 來源: 題型:
【題目】為了解某校學生對《最強大腦》、《朗讀者》、《中國詩詞大會》、《出彩中國人》四個電視節目的喜愛情況,隨機抽取了x名學生進行調查統計(要求每名學生選出并且只能選出一個自己最喜愛的節目),并將調查結果繪制成如下統計圖表: 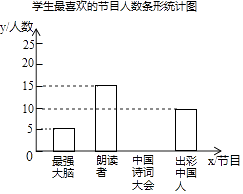
學生最喜愛的節目人數統計表
節目 | 人數(名) | 百分比 |
最強大腦 | 5 | 10% |
朗讀者 | 15 | b% |
中國詩詞大會 | a | 40% |
出彩中國人 | 10 | 20% |
根據以上提供的信息,解答下列問題:
(1)x= , a= , b=;
(2)補全上面的條形統計圖;
(3)若該校共有學生1000名,根據抽樣調查結果,估計該校最喜愛《中國詩詞大會》節目的學生有多少名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 邊長為
邊長為![]() 的等邊三角形
的等邊三角形![]() 的頂點
的頂點![]() 分別在邊
分別在邊![]() ,
,![]() 上當
上當![]() 在邊
在邊![]() 上運動時,
上運動時,![]() 隨之在邊
隨之在邊![]() 上運動,等邊三角形的形狀保持不變,運動過程中,點
上運動,等邊三角形的形狀保持不變,運動過程中,點![]() 到點
到點![]() 的最大距離為( )
的最大距離為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年5月14日至15日,“一帶一路”國際合作高峰論壇在北京舉行.本屆論壇期間,中國同30多個國家簽署經貿合作協議.某廠準備生產甲、乙兩種商品共8萬件銷往“一帶一路”沿線國家和地區.已知2件甲種商品與3件乙種商品的銷售收入相同,3件甲種商品比2件乙種商品的銷售收入多1500元.
(1)甲種商品與乙種商品的銷售單價各多少元?
(2)若甲、乙兩種商品的銷售總收入不低于5400萬元,則至少銷售甲種商品多少萬件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】林叢同學調查了全班50名同學分別喜歡相聲、小品、歌曲、舞蹈節目的情況,并制成下面的統計表:
最喜歡的節目類型 | 劃記 | 人數 | 百分比 |
相聲 | 正 | 13 | 26% |
小品 | 正正正一 | 21 | 42% |
歌曲 | 正正 | 10 | 28% |
舞蹈 | 正一 | 6 | 12% |
在上表所給的數據中,僅有一類節目的統計是完全正確的,則該項目統計類別是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少?”共有4個選題.
A.1.5小時以上 B.1~1.5小時 C.0.5~1小時 D.0.5小時以下
請你根據統計圖提供的信息,解答以下問題:
(1)本次一共調查了多少名學生?
(2)將條形統計圖選項B補充完整;
(3)若該校有3000名學生,你估計全校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下?
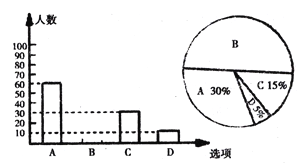
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩家綠化養護公司各自推出了校園綠化養護服務的收費方案.
甲公司方案:每月的養護費用y(元)與綠化面積x(平方米)是一次函數關系,如圖所示.
乙公司方案:綠化面積不超過1000平方米時,每月收取費用5500元;綠化面積超過1000平方米時,每月在收取5500元的基礎上,超過部分每平方米收取4元.

(1)求如圖所示的y與x的函數解析式;(不要求寫取值范圍)
(2)如果某學校目前的綠化面積是1200平方米.試通過計算說明:選擇哪家公司的服務,每月的綠化養護費用較少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知長方形ABCD,AB=1,BC=2,點M為矩形內一點,點E為BC邊上任意一點,則MA+MD+ME的最小值為( )

A. 1 B. 1+![]() C. 2+
C. 2+![]() D. 3
D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠現有甲種原料360千克,乙種原料290千克,計劃利用這兩種原料生產A、B兩種產品共50件,已知生產一件A種產品用甲種原料9千克,乙種原料3千克,可獲利700元;生產一件B種產品用甲種原料4千克,乙種原料10千克,可獲利1200元.
(1)按要求安排A、B兩種產品的生產件數,有哪幾種方案?請你設計出來;
(2)設生產A、B兩種產品總利潤為y元,其中一種產品生產件數為x件,試寫出y與x之間的函數關系式,并利用函數的性質說明那種方案獲利最大?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com