Question

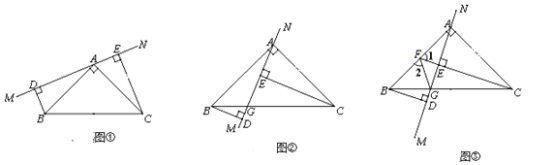
【題目】如圖①，在中， ， ， ． 是經過點的直線， 于， 于．

（1）求證： ．

（2）若將繞點旋轉，使與相交于點 (如圖②)，其他條件不變，

求證： ．

（3）在(2)的情況下，若的延長線過的中點（如圖③），連接，

求證： ．

Answer 1

【答案】答案見解析

【解析】試題分析：（1）首先證明∠DBA＝∠EAC，再證明△ADB≌△CEA，然后根據全等三角形的性質可得BD=AE；

（2）首先證明∠BAD=∠ACE，再證明△ABD≌△ACE，根據全等三角形對應邊相等可得BD=AE；

（3）首先證明△ACF≌△ABP，然后再證明△BFG≌△BPG，再根據全等三角形對應角相等可得∠BPG=∠BFG，再根據等量代換可得結論∠1=∠2．

試題解析：

（1）∵BD⊥MN，CE⊥MN

∴∠BDA＝∠AEC＝90°

∴∠DBA+∠DAB＝90°

∵∠BAC＝90°

∴∠DAB +∠EAC＝90°

∴∠DBA＝∠EAC

∵AB = AC

∴△ADB≌△CEA（AAS）

∴BD＝AE

（2）∵BD⊥MN，CE⊥MN

∴∠BDA＝∠AEC＝90°

∴∠DBA+∠DAB＝90°

∵∠BAC＝90°

∴∠DAB +∠EAC＝90°

∴∠DBA＝∠EAC

∵AB = AC

∴△ADB≌△CEA（AAS）

∴BD＝AE

（3）過B作BP//AC交MN于P,如圖所示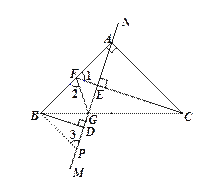

∵BP//AC

∴∠PBA+∠BAC＝90°

∵∠BAC＝90°

∴∠PBA＝∠BAC＝90°

由（2）得：△ADB≌△CEA

∴∠BAP＝∠ACF

∵AB＝AC

∴△ACF≌△ABP（ASA）

∴∠1＝∠3

∴AF=BP

∵AB的中點F

∵BF＝AF

∴BF＝BP

∵∠ABC=45°

又∵∠PBA＝90°

∴∠PBG＝∠PBA－∠ABC =45°

∴∠ABC＝∠PBG

∵BG=BG

∴△BFG≌△BPG（SAS）

∴∠2＝∠3

∵∠1＝∠3

∴∠1＝∠2