Question

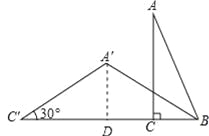
【題目】如圖，書桌上的一種新型臺歷和一塊主板AB、一個架板AC和環(huán)扣（不計寬度，記為點A）組成，其側面示意圖為△ABC，測得AC⊥BC，AB=5cm，AC=4cm，現(xiàn)為了書寫記事方便，須調(diào)整臺歷的擺放，移動點C至C′，當∠C′=30°時，求移動的距離即CC′的長（或用計算器計算，結果取整數(shù)，其中 =1.732， =4.583）

Answer 1

【答案】5cm

【解析】試題分析：過點A′作A′D⊥BC′，垂足為D，先在△ABC中，由勾股定理求出BC=3cm，再解Rt△A′DC′，得出A′D=2cm，C′D=2cm，在Rt△A′DB中，由勾股定理求出BD=cm，然后根據(jù)CC′=C′D+BD﹣BC，將數(shù)據(jù)代入，即可求出CC′的長．

試題解析：過點A′作A′D⊥BC′，垂足為D．

在△ABC中，∵AC⊥BC，AB=5cm，AC=4cm，∴BC=3cm．

當動點C移動至C′時，A′C′=AC=4cm．在△A′DC′中，∵∠C′=30°，∠A′DC′=90°，

∴A′D=A′C′=2cm，C′D=A′D=2cm．

在△A′DB中，∵∠A′DB=90°，A′B=5cm，A′D=2cm，∴BD==cm，

∴CC′=C′D+BD﹣BC=2+﹣3，∵=1.732，=4.583，∴CC′=2×1.732+4.583﹣3≈5．

故移動的距離即CC′的長約為5cm．