Question

【題目】如圖在矩形ABCD中，AB= AD,點E、F分別在AB、AD上且不與頂點A、B、D重合， , 圓O過A、E、F三點。

（1）求證：圓O與CE相切于點E.

（2）如圖1，若AF=2FD，且，求的值。

（3）如圖2，若EF=EC，且圓O與邊CD相切，求的值。

Answer 1

【答案】（1）證明見解析；（2）；（3）

【解析】（1）由四邊形ABCD是矩形證明∠FEC=90°即可；（2）在直角三角形中利用三角函數(shù)求解；（3）利用三角形中位線、勾股定理和題意可列方程求出n的值．

(1)證明：∵四邊形ABCD是矩形，∴∠B=90°，

∠BCE+∠BEC=90°，

又∵∠AEF=∠BCE，∵∠AEF+∠BEC=90°，

∴∠FEC=90°，∴⊙O與CE相切．

（2）∵AF=2FD,設(shè)FD=a。則AF=2a，

在直角三角形AEC中，∵∠AEF=30°，

∴∠BCE=30°．

∴EF=4a，由勾股定理：AE= ，

．

∴BC=3a，又在直角三角形EBC中，

，

.

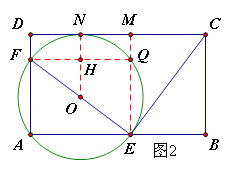
過E作EMDC于M,因為圓O與CD相切，設(shè)切點為N，連接ON,又過F作FQEM交ON于H， FE=EC, EFEC, ，

根據(jù)題意和作圖，可設(shè)AE=BC=ME=AD= ，AF=QE=EB= ，

易證明OH為的中位線，OH=，

2ON=EF=，

由勾股定理和題意可列方程：

，

化簡：

．

“點睛”本題考查了直線與圓的位置關(guān)系，將方程與幾何融合在一起，利用勾股定理和方程組解答；解答本題需要我們熟練各部分的內(nèi)容，對學生的綜合能力要求較高，一定要注意將所學知識貫穿起來．