
【題目】在平面直角坐標系中,點A,B分別是x軸正半軸與y軸正半軸上一點,OA=m,OB=n,以AB為邊在第一象限內作正方形ABCD.
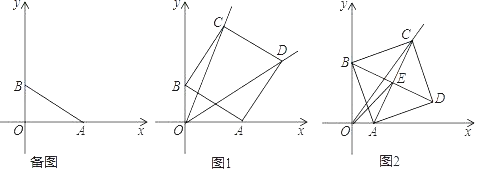
(1)若m=4,n=3,直接寫出點C與點D的坐標;
(2)點C在直線y=kx(k>1且k為常數)上運動.
①如圖1,若k=2,求直線OD的解析式;
②如圖2,連接AC、BD交于點E,連接OE,若OE=2![]() OA,求k的值.
OA,求k的值.
【答案】(1)C(3,7),D(7,4);(2)①y=![]() x;②
x;②![]() .
.
【解析】
(1)根據題意把m=4,n=3代入解答即可;
(2)①利用待定系數法確定函數關系式即可;
②根據B、D坐標表示出E點坐標,由勾股定理可得到m、n之間的關系式,用m表示出C點坐標,根據函數關系式解答即可.
解:(1)∵OA=m,OB=n,以AB為邊在第一象限內作正方形ABCD,
∴C(n,m+n),D(m+n,m),
把m=4,n=3代入可得:
C(3,7),D(7,4),
(2)①設C(a,2a),由題意可得:![]() ,
,
解得:m=n=a,
∴D(2a,a),
∴直線OD的解析式為:y=![]() x,
x,
②由B(0,n),D(m+n,m),
可得:E(![]() ,
,![]() ),OE=
),OE=![]() OA,
OA,
∴(![]() )2+(
)2+(![]() )2=8m2,
)2=8m2,
可得:(m+n)2=16m2,
∴m+n=4m,n=3n,
∴C(3m,4m),
∴直線OC的解析式為:y=![]() x,
x,
可得:k=![]() .
.
故答案為:(1)C(3,7),D(7,4);(2)①y=![]() x;②
x;②![]() .
.


科目:初中數學 來源: 題型:
【題目】新冠肺炎疫情爆發以來,學生們都在家里上網課,為了了解學生在家上網課使用的設備種類,47中學校初二學年在本學年內隨機抽取部分學生進行問卷調查,要求學生在“臺式電腦、筆記本電腦、平板電腦、手機、網絡電視”五類設備中,選取自己經常使用的一種(必選且只選一種),學年將收集到的調查結果適當整理后,繪制成如圖所示的不完整的統計圖.請根據圖中所給的信息解答下列問題:

(1)在這次調查中,一共抽取了多少名學生?
(2)請通過計算補全條形統計圖;
(3)若47中學初二學年共有1000名學生,估計該校初二學年使用手機上課的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一副直角三角尺疊放如圖 1 所示,現將 45°的三角尺ADE 固定不動,將含 30°的三角尺 ABC 繞頂點 A 順時針轉動(旋轉角不超過 180 度),使兩塊三角尺至少有一組邊互相平行.如圖 2:當∠BAD=15°時,BC∥DE.則∠BAD(0°<∠BAD<180°)其它所有可能符合條件的度數為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“大美武漢,暢游江城”.某校數學興趣小組就“最想去的武漢市旅游景點”隨機調查了本校部分學生,要求每位同學選擇且只能選擇一個最想去的景點,下面是根據調查結果進行數據整理后繪制出的不完整的統計圖:
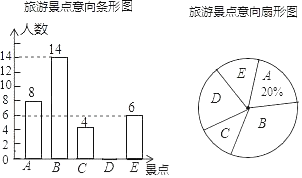
請根據圖中提供的信息,解答下列問題:
(1)求被調查的學生總人數;
(2)補全條形統計圖,并求扇形統計圖中表示“最想去景點D”的扇形圓心角的度數;
(3)若該校共有1200名學生,請估計“最想去景點B“的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
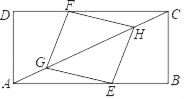
【題目】如圖,矩形ABCD中,點E,F分別在邊AB與CD上,點G、H在對角線AC上,AG=CH,BE=DF.
(1)求證:四邊形EGFH是平行四邊形;
(2)若EG=EH,AB=8,BC=4.求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,O為原點,一次函數y1=x+m與反比例函數y2= ![]() 的圖象相交于A(2,1),B(n,﹣2)兩點,與x軸交于點C.
的圖象相交于A(2,1),B(n,﹣2)兩點,與x軸交于點C.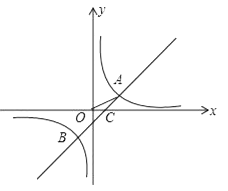
(1)求反比例函數解析式和點B坐標;
(2)當x的取值范圍是時,有y1>y2 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形邊長為1的方格紙內將△ABC經過一次平移后得到△A′B′C′,圖中標出了點B的對應點B′.根據下列條件,利用格點和三角尺畫圖:
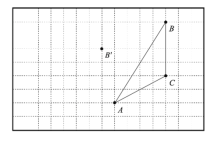
(1)補全△A′B′C′;
(2)請在AC邊上找一點D,使得線段BD平分△ABC的面積,在圖上作出線段BD;
(3)利用格點在圖中畫出AC邊上的高線BE;
(4)求△ABD的面積_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設M(m,n)在反比例函數y=﹣ ![]() 上,其中m是分式方程
上,其中m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,將M點先向上平移4個單位,再向左平移1個單位,得到點N.若點M,N都在直線y=kx+b上,直線解析式為( )
的根,將M點先向上平移4個單位,再向左平移1個單位,得到點N.若點M,N都在直線y=kx+b上,直線解析式為( )
A.y=﹣ ![]() x﹣
x﹣ ![]()
B.y= ![]() x+
x+ ![]()
C.y=4x﹣5
D.y=﹣4x+5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用我們學過的知識,可以導出下面這個形式優美的等式:a2+b2+c2﹣ab﹣bc﹣ac=![]() [(a﹣b)2+(b﹣c)2+(a﹣c)2],該等式從左到右的變形,不僅保持了結構的對稱性,還體現了數學的和諧、簡潔、美觀.
[(a﹣b)2+(b﹣c)2+(a﹣c)2],該等式從左到右的變形,不僅保持了結構的對稱性,還體現了數學的和諧、簡潔、美觀.
(1)請你檢驗說明這個等式的正確性.
(2)若a=2019,b=2020,c=2021,你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值嗎?
(3)若a﹣b=![]() ,b﹣c=
,b﹣c=![]() ,且a2+b2+c2=1,求ab+bc+ac的值.
,且a2+b2+c2=1,求ab+bc+ac的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com