【題目】如圖，四邊形紙片ABCD中，∠A=70°，∠B=80°，將紙片折疊，使C，D落在AB邊上的C′，D′處，折痕為MN，則∠AMD′+∠BNC′=（ ）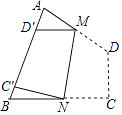 
A.50°
B.60°
C.70°
D.80°
【答案】B
【解析】解：四邊形紙片ABCD中，∠A=70°，∠B=80°， ∴∠D+∠C=360°﹣∠A﹣∠B=210°，
∵將紙片折疊，使C，D落在AB邊上的C，D′處，
∴∠MD′B=∠D，∠NC′A=∠C，
∴∠MD′B+∠NC′A=210，
∴∠AD′M+∠BC′N=150°，
∴∠AMD′+∠BNC′=360°﹣∠A﹣∠B﹣∠AD′M﹣∠BC′N=60°，
故選B．
根據四邊形的內角和得到∠D+∠C=360°﹣∠A﹣∠B=210°，由折疊的性質得到∠MD′B=∠D，∠NC′A=∠C，得到∠MD′B+∠NC′A=210，根據平角的定義得到∠AD′M+∠BN′N=150°，根據三角形的內角和即可得到結論．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如果點
將線段
分成兩條相等的線段
和
，那么叫做線段的二等分點(中點);如果點
，
將線段分成三條相等的線段
，
和
，那么，叫做線段的三等分點;…;依此類推，如果點
將線段分成
條相等的線段
，那么叫做線段的等分點，如圖①所示.
已知點
在直線
的同側，請回答下列問題.
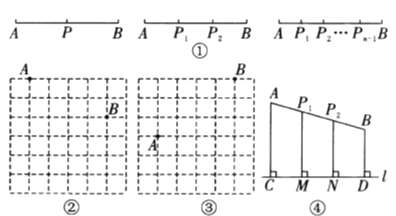
(1)在所給邊長為個單位長度的正方形網格中，探究:
①如圖②，若點
到直線的距離分別是4個單位長度和2個單位長度，則線段 的中點到直線的距離是 個單位長度;
②如圖③，若點到直線的距離分別是2個單位長度和5個單位長度，則線段 的中點到直線的距離是 個單位長度;
③由①②可以發現結論:若點到直線的距離分別是
個單位長度和
個單位長度，則線段 的中點到直線的距離是 個單位長度.
(2)如圖④，若點到直線的距離分別是
和
，利用(1)中的結論求線段的三等分點，到直線的距離分別是 .
(3)若點到直線的距離分別是和，點為線段的等分點，直接寫出第
個等分點
到直線的距離.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y=ax2+bx+c與兩坐標軸的交點分別為A、B、C，且OA=OC=1，則下列關系中正確的是（ ） 
A.a+b=﹣1
B.a﹣b=﹣1
C.b＜2a
D.ac＜0
查看答案和解析>>
科目：初中數學 來源： 題型：
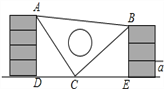
【題目】課間，小明拿著老師的等腰三角板玩，不小心掉到兩墻之間，如圖．
（1）求證：△ADC≌△CEB；
（2）從三角板的刻度可知AC=25cm，請你幫小明求出砌墻磚塊的厚度a的大小（每塊磚的厚度相等）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某中學七年級四班的同學在體檢中測量了自己的身高，并求出了該班同學的平均身高．
（1）下表給出了該班5名同學的身高情況（單位：cm），試完成該表，并求出該班同學的平均身高．
姓名 | 劉杰 | 劉濤 | 李明 | 張春 | 劉建 |
身高 | 161 |
|
| 165 | 155 |
身高與全班同 學平均身高差 | +3 | ﹣1 | 0 |
|
|
（2）誰最高？誰最矮？
（3）計算這5名同學的平均身高是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在一次測繪活動中，某同學站在點A處觀測停放于B、C兩處的小船，測得船B在點A北偏東75°方向150米處，船C在點A南偏東15°方向120米處，則船B與船C之間的距離為______米（精確到0.1
）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，六邊形ABCDEF的內角都相等，∠DAB＝60°，AB＝DE，則下列結論：①AB∥DE；②EF∥AD∥BC；③AF＝CD；④四邊形ACDF是平行四邊形；⑤六邊形ABCDEF既是中心對稱圖形，又是軸對稱圖形．其中成立的個數是( )
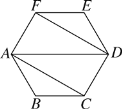
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目：初中數學 來源： 題型：
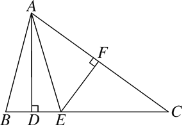
【題目】如圖，△ABC中，AD⊥BC于點D，EF垂直平分AC，交AC于點F，交BC于點E，且BD＝DE，連接AE.
(1)若∠BAE＝30°，求∠C的度數；
(2)若△ABC的周長為13cm，AC＝6cm，求DC的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
