【題目】如圖，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分線與AB的中垂線交于點O，點C沿EF折疊后與點O重合，則∠CEF的度數是 ．
【答案】50°.
【解析】
利用全等三角形的判定以及垂直平分線的性質得出∠OBC＝40°，以及∠OBC＝∠OCB＝40°，再利用翻折變換的性質得出EO＝EC，∠CEF＝∠FEO，進而求出即可;
連接BO，
∵AB＝AC，AO是∠BAC的平分線，
∴AO是BC的中垂線.
∴BO＝CO.
∵∠BAC＝50°，∠BAC的平分線與AB的中垂線交于點O，
∴∠OAB＝∠OAC＝25°.
∵等腰△ABC中， AB＝AC，∠BAC＝50°，
∴∠ABC＝∠ACB＝65°.
∴∠OBC＝65°－25°＝40°.
∴∠OBC＝∠OCB＝40°.
∵點C沿EF折疊后與點O重合，
∴EO＝EC，∠CEF＝∠FEO.
∴在△OEC中，
∠CEF＝∠FEO＝（180°－2×40°）÷2＝50°.
科目：初中數學 來源： 題型：
【題目】如圖(十九)，用四個螺絲將四條不可彎曲的木條圍成一個木框，不計螺絲大小，其中相鄰兩螺絲的距離依序為2、3、4、6，且相鄰兩木條的夾角均可調整。若調整木條的夾角時不破壞此木框，則任兩螺絲的距離之最大值為何？
(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面內，給定∠AOB=60°，及OB邊上一點C，如圖所示．到射線OA，OB距離相等的所有點組成圖形G，線段OC的垂直平分線交圖形G于點D，連接CD．
（1）依題意補全圖形；直接寫出∠DCO的度數；
（2）過點D作OD的垂線，交OA于點E，OB于點F．求證：CF=DE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，
，已知
中，
，
，的頂點
、
分別在邊
、
上，當點在邊上運動時，隨之在上運動，的形狀始終保持不變，在運動的過程中，點
到點
的最小距離為（ ）
A. 5 B. 7 C. 12 D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】連接正八邊形的三個頂點，得到如圖所示的圖形，下列說法錯誤的是（ ）
A. 
是等邊三角形
B. 連接
，則分別平分
和
C. 整個圖形是軸對稱圖形，但不是中心對稱圖形
D. 四邊形
與四邊形
的面積相等
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，有一張矩形紙片，長10cm，寬6cm，在它的四角各減去一個同樣的小正方形，然后折疊成一個無蓋的長方體紙盒．若紙盒的底面（圖中陰影部分）面積是32cm2，求剪去的小正方形的邊長．設剪去的小正方形邊長是xcm，根據題意可列方程為（ ）
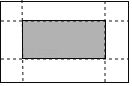
A. 10×6﹣4×6x=32 B. （10﹣2x）（6﹣2x）=32
C. （10﹣x）（6﹣x）=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某學校計劃在總費用2300元的限額內，租用客車送234名學生和6名教師集體外出活動，每輛客車上至少要有1名教師.現有甲、乙兩種大客車，它們的載客量和租金如下表所示.
甲種客車 | 乙種客車 | |
載客量/(人/輛) | 45 | 30 |
租金/(元/輛) | 400 | 280 |
(1)共需租多少輛客車?
(2)請給出最節省費用的租車方案.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市計劃建造一座如圖設計的塔形建筑物作為市標，最底層的圓柱形的底面半徑為
，高為
米，再上去的圓柱形底面半徑以
的比例縮小，而樓層的高度也以同樣的比例縮小，那么要使得建筑物的表面積不超過
平方米（表面積不包括最底層的底面積），樓層最高為________層．
取
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
