Question

【題目】如圖，在平面直角坐標系中，點O為坐標原點，直線l與拋物線y=mx2+nx相交于A（1，3 ），B（4，0）兩點．

（1）求出拋物線的解析式；
（2）在坐標軸上是否存在點D，使得△ABD是以線段AB為斜邊的直角三角形？若存在，求出點D的坐標；若不存在，說明理由；
（3）點P是線段AB上一動點，（點P不與點A、B重合），過點P作PM∥OA，交第一象限內的拋物線于點M，過點M作MC⊥x軸于點C，交AB于點N，若△BCN、△PMN的面積S△BCN、S△PMN滿足S△BCN=2S△PMN ， 求出 的值，并求出此時點M的坐標．

Answer 1

【答案】
（1）

解：∵A（1，3 ），B（4，0）在拋物線y=mx2+nx的圖象上，

∴ ，解得 ，

∴拋物線解析式為y=﹣ x2+4 x；

（2）

解：存在三個點滿足題意，理由如下：

當點D在x軸上時，如圖1，過點A作AD⊥x軸于點D，

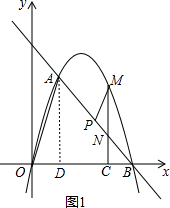
∵A（1，3 ），

∴D坐標為（1，0）；

當點D在y軸上時，設D（0，d），則AD2=1+（3 ﹣d）2，BD2=42+d2，且AB2=（4﹣1）2+（3 ）2=36，

∵△ABD是以AB為斜邊的直角三角形，

∴AD2+BD2=AB2，即1+（3 ﹣d）2+42+d2=36，解得d= ，

∴D點坐標為（0， ）或（0， ）；

綜上可知存在滿足條件的D點，其坐標為（1，0）或（0， ）或（0， ）；

（補充方法：可用A，B點為直徑作一個圓，圓與坐標軸的交點即為答案）

（3）

解：如圖2，過P作PF⊥CM于點F，

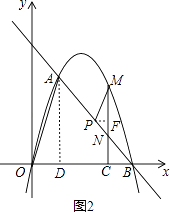
∵PM∥OA，

∴Rt△ADO∽Rt△MFP，

∴ = =3 ，

∴MF=3 PF，

在Rt△ABD中，BD=3，AD=3 ，

∴tan∠ABD= ，

∴∠ABD=60°，設BC=a，則CN= a，

在Rt△PFN中，∠PNF=∠BNC=30°，

∴tan∠PNF= = ，

∴FN= PF，

∴MN=MF+FN=4 PF，

∵S△BCN=2S△PMN，

∴ a2=2× ×4 PF2，

∴a=2 PF，

∴NC= a=2 PF，

∴ = = ，

∴MN= NC= × a= a，

∴MC=MN+NC=（ + ）a，

∴M點坐標為（4﹣a，（ + ）a），

又M點在拋物線上，代入可得﹣ （4﹣a）2+4 （4﹣a）=（ + ）a，

解得a=3﹣ 或a=0（舍去），

OC=4﹣a= +1，MC=2 + ，

∴點M的坐標為（ +1，2 + ）．

【解析】（1）由A、B兩點的坐標，利用待定系數法可求得拋物線解析式；（2）分D在x軸上和y軸上，當D在x軸上時，過A作AD⊥x軸，垂足D即為所求；當D點在y軸上時，設出D點坐標為（0，d），可分別表示出AD、BD，再利用勾股定理可得到關于d的方程，可求得d的值，從而可求得滿足條件的D點坐標；（3）過P作PF⊥CM于點F，利用Rt△ADO∽Rt△MFP以及三角函數，可用PF分別表示出MF和NF，從而可表示出MN，設BC=a，則可用a表示出CN，再利用S△BCN=2S△PMN ， 可用PF表示出a的值，從而可用PF表示出CN，可求得 的值；借助a可表示出M點的坐標，代入拋物線解析式可求得a的值，從而可求出M點的坐標．
【考點精析】關于本題考查的二次函數的性質，需要了解增減性：當a>0時，對稱軸左邊，y隨x增大而減小；對稱軸右邊，y隨x增大而增大；當a<0時，對稱軸左邊，y隨x增大而增大；對稱軸右邊，y隨x增大而減小才能得出正確答案．