
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于點
于點![]() ,
,![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,若
,若![]() ,則
,則![]() _____.
_____.
【答案】4
【解析】
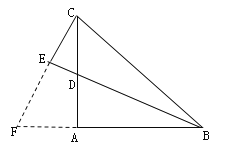
首先延長CE和BA交于F,由BD平分∠ABC得出∠CBE=∠ABE=∠FBE,又由CE⊥BD即CE⊥BE,得出∠BEC=∠BEF=90°,然后加上BE=BE,即可判定△BEC≌△BEF(ASA)得出CE=EF=![]() CF,再通過等角轉換得出∠F=∠CDE,由對頂角相等∠BDA=∠CDE,進而得出∠BDA=∠F,∠FAC=∠DAB=90°,加上AB=AC,判定△ABD≌△ACF(AAS),得出BD=CF=2CE,即可得解.
CF,再通過等角轉換得出∠F=∠CDE,由對頂角相等∠BDA=∠CDE,進而得出∠BDA=∠F,∠FAC=∠DAB=90°,加上AB=AC,判定△ABD≌△ACF(AAS),得出BD=CF=2CE,即可得解.
延長CE和BA交于F,如圖所示
∵BD平分∠ABC
∴∠CBE=∠ABE=∠FBE
∵CE⊥BD即CE⊥BE
∴∠BEC=∠BEF=90°
∵BE=BE
∴△BEC≌△BEF(ASA)
∴CE=EF=![]() CF
CF
∵∠BAC=90°,那么∠FAC=∠CED=90°
∴∠CDE=90°-∠ACF
∠F=90°-∠ACF
∴∠F=∠CDE
∵∠BDA=∠CDE(對頂角相等)
∴∠BDA=∠F
∵∠FAC=∠DAB=90°
AB=AC
∴△ABD≌△ACF(AAS)
∴BD=CF=2CE
即CE=![]() BD=4
BD=4
故答案為4.


科目:初中數學 來源: 題型:
【題目】如圖所示,以正方形![]() 的頂點
的頂點![]() 為圓心的弧恰好與對角線
為圓心的弧恰好與對角線![]() 相切,以頂點
相切,以頂點![]() 為圓心,正方形的邊長為半徑的弧,已知正方形的邊長為
為圓心,正方形的邊長為半徑的弧,已知正方形的邊長為![]() ,則圖中陰影部分的面積為( )
,則圖中陰影部分的面積為( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A,B兩地相距200千米,甲車從A地出發勻速行駛到B地,乙車從B地出發勻速行駛到A地.乙車行駛1小時后,甲車出發,兩車相向而行.設行駛時間為x小時(0≤x≤5),甲、乙兩車離A地的距離分別為y1,y2千米,y1,y2與x之間的函數關系圖象如圖1所示.根據圖象解答下列問題:
(1)求y1,y2與x的函數關系式;
(2)乙車出發幾小時后,兩車相遇?相遇時,兩車離A地多少千米?
(3)設行駛過程中,甲、乙兩車之間的距離為s千米,在圖2的直角坐標系中,已經畫出了s與x之間的部分函數圖象.
①圖中點P的坐標為(1,m),則m= ;
②求s與x的函數關系式,并在圖2中補全整個過程中s與x之間的函數圖象.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=﹣![]() x+2的圖象交x軸、y軸分別于點A,B,交直線y=kx于P.
x+2的圖象交x軸、y軸分別于點A,B,交直線y=kx于P.
(1)求點A、B的坐標;
(2)若OP=PA,求P點坐標及k的值.
(3)在(2)的條件下,C是直線BP上一動點,CE⊥x軸于E,交直線DP于D,若CD=3ED,直接寫出C點的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
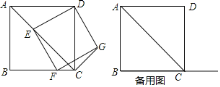
【題目】四邊形![]() 為正方形,點
為正方形,點![]() 為線段
為線段![]() 上一點,連接
上一點,連接![]() ,過點
,過點![]() 作
作![]() ,交射線
,交射線![]() 于點
于點![]() ,以
,以![]() 、
、![]() 為鄰邊作矩形
為鄰邊作矩形![]() ,連接
,連接![]() .
.
![]() 如圖
如圖![]() ,求證:矩形
,求證:矩形![]() 是正方形;
是正方形;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的長度;
的長度;
![]() 當線段
當線段![]() 與正方形
與正方形![]() 的某條邊的夾角是
的某條邊的夾角是![]() 時,直接寫出
時,直接寫出![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖①,在四邊形![]() 中,
中,![]() ,點
,點![]() 是
是![]() 的中點,若
的中點,若![]() 是
是![]() 的平分線,試判斷
的平分線,試判斷![]() ,
,![]() ,
,![]() 之間的等量關系.
之間的等量關系.
解決此問題可以用如下方法:延長![]() 交
交![]() 的延長線于點
的延長線于點![]() ,易證
,易證![]() 得到
得到![]() ,從而把
,從而把![]() ,
,![]() ,
,![]() 轉化在一個三角形中即可判斷.
轉化在一個三角形中即可判斷.
![]() ,
,![]() ,
,![]() 之間的等量關系________;
之間的等量關系________;
(2)問題探究:如圖②,在四邊形![]() 中,
中,![]() ,
,![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,點
,點![]() 是
是![]() 的中點,若
的中點,若![]() 是
是![]() 的平分線,試探究
的平分線,試探究![]() ,
,![]() ,
,![]() 之間的等量關系,并證明你的結論.
之間的等量關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=50°,∠B=∠C,點D,E,F分別在邊BC,CA,AB上,且滿足BF=CD,BD=CE,∠BFD=30°,則∠FDE的度數為( )

A.75°B.80°C.65°D.95°
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com