
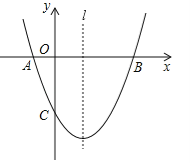
【題目】如圖,已知拋物線![]() (a≠0)經過A(﹣1,0)、B(3,0)、C(0,﹣3)三點,直線l是拋物線的對稱軸.
(a≠0)經過A(﹣1,0)、B(3,0)、C(0,﹣3)三點,直線l是拋物線的對稱軸.
(1)求拋物線的函數關系式;
(2)設點P是直線l上的一個動點,當點P到點A、點B的距離之和最短時,求點P的坐標;
(3)點M也是直線l上的動點,且△MAC為等腰三角形,請直接寫出所有符合條件的點M的坐標.
【答案】(1)![]() ;(2)P(1,0);(3).
;(2)P(1,0);(3).
【解析】(1)將A(﹣1,0)、B(3,0)、C(0,﹣3)代入拋物線![]() 中,得:
中,得: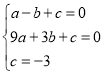
,解得: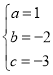 ,故拋物線的解析式:
,故拋物線的解析式:![]() .
.
(2)當P點在x軸上,P,A,B三點在一條直線上時,點P到點A、點B的距離之和最短,此時x=![]() =1,故P(1,0);
=1,故P(1,0);
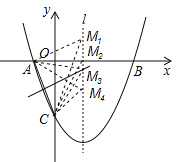
(3)如圖所示:拋物線的對稱軸為:x=![]() =1,設M(1,m),已知A(﹣1,0)、C(0,﹣3),則:
=1,設M(1,m),已知A(﹣1,0)、C(0,﹣3),則:
![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =10;
=10;
①若MA=MC,則![]() ,得:
,得:![]() =
=![]() ,解得:m=﹣1;
,解得:m=﹣1;
②若MA=AC,則![]() ,得:
,得:![]() =10,得:m=
=10,得:m=![]() ;
;
③若MC=AC,則![]() ,得:
,得:![]() =10,得:
=10,得:![]() ,
,![]() ;
;
當m=﹣6時,M、A、C三點共線,構不成三角形,不合題意,故舍去;
綜上可知,符合條件的M點,且坐標為 M(1,![]() )(1,
)(1,![]() )(1,﹣1)(1,0).
)(1,﹣1)(1,0).


科目:初中數學 來源: 題型:
【題目】解方程組的基本思想是_________,也就是把二元一次方程組轉化為______________. 消元的方法有:_____________、_______________等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB, OE平分∠AOC, OF平分∠BOC.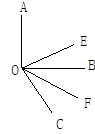
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度數;
(2)猜想∠EOF與∠AOB的數量關系;
(3)若∠AOB+∠EOF=156°,則∠EOF是多少度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙兩動點分別從正方形ABCD的頂點A、C同時沿正方形的邊開始移動,甲點依順時針方向環行,乙點依逆時針方向環行.若甲的速度是乙的速度的3倍,則它們第2015次相遇在邊 上.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com