欧美xxxx网站,亚洲爱爱综合网,99免在线观看免费视频高清

【題目】如圖，已知AE=CF，∠AFD=∠CEB，那么添加下列一個條件后，仍無法判定△ADF≌△CBE的是（）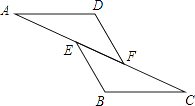

A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC

【答案】B
【解析】解：∵AE=CF，
∴AE+EF=CF+EF，
∴AF=CE，
A、∵在△ADF和△CBE中

∴△ADF≌△CBE（ASA），正確，故本選項錯誤；
B、根據AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，錯誤，故本選項正確；
C、∵在△ADF和△CBE中

∴△ADF≌△CBE（SAS），正確，故本選項錯誤；
D、∵AD∥BC，
∴∠A=∠C，
∵在△ADF和△CBE中

∴△ADF≌△CBE（ASA），正確，故本選項錯誤；
故選B．
求出AF=CE，再根據全等三角形的判定定理判斷即可．

練習冊系列答案

奪分A計劃小學畢業升學總復習系列答案

小學畢業升學總復習金榜小狀元系列答案

同步測評卷期末卷系列答案

小學生10分鐘口算測試100分系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：初中數學 來源： 題型：

【題目】根據給出的數軸及已知條件，解答下面的問題：

（1）已知點A，B，C表示的數分別為1，﹣ ，﹣3觀察數軸，與點A的距離為3的點表示的數是， B，C兩點之間的距離為；
（2）若將數軸折疊，使得A點與C點重合，則與B點重合的點表示的數是；若此數軸上M，N兩點之間的距離為2015（M在N的左側），且當A點與C點重合時，M點與N點也恰好重合，則M，N兩點表示的數分別是：M ， N；
（3）若數軸上P，Q兩點間的距離為m（P在Q左側），表示數n的點到P，Q兩點的距離相等，則將數軸折疊，使得P點與Q點重合時，P，Q兩點表示的數分別為：P ， Q（用含m，n的式子表示這兩個數）．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】設⊙O的半徑為r，P到圓心的距離為d不大于r，則點P在( )

A. 在⊙O內B. 在⊙O外C. 不在⊙O內D. 不在⊙O外

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】(12分)如圖，以△ABC的BC邊上一點O為圓心的圓，經過A、B兩點，且與BC邊交于點E，D為BE的下半圓弧的中點，連接AD交BC于F，AC=FC．

(1)求證：AC是⊙O的切線；

(2)已知圓的半徑R=5，EF=3，求DF的長．

查看答案和解析>>

科目：初中數學 來源： 題型：

【題目】閱讀
（1）閱讀理解：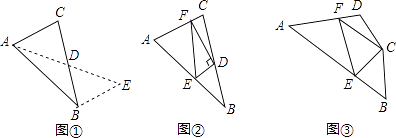

如圖①，在△ABC中，若AB=10，AC=6，求BC邊上的中線AD的取值范圍．
解決此問題可以用如下方法：延長AD到點E使DE=AD，再連接BE（或將△ACD繞著點D逆時針旋轉180°得到△EBD），把AB，AC，2AD集中在△ABE中，利用三角形三邊的關系即可判斷．
中線AD的取值范圍是；
（2）問題解決：
如圖②，在△ABC中，D是BC邊上的中點，DE⊥DF于點D，DE交AB于點E，DF交AC于點F，連接EF，求證：BE+CF＞EF；
（3）問題拓展：
如圖③，在四邊形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以C為頂點作一個70°角，角的兩邊分別交AB，AD于E，F兩點，連接EF，探索線段BE，DF，EF之間的數量關系，并加以證明．